Exercice en maths sur seconde degré
-
Ccestmoilesgars dernière édition par Casebas
Bonsoir j’ai besoin de l’aide
Exercice 1
Un bricoleur souhaite r ́ealiser une gouttière pour sa cabane de jardin mesurant 6 m de long. Il dispose d’une feuille de m ́etal rectangulaire de 6 m de long et de 14 cm de large. Il compte plier chaque cˆot ́e de la feuille en les relevant perpendiculairement à la feuille. On désigne par x la longueur en cm d’un côté relevé et V (x) le volume en cm3 de la gouttière. Le bricoleur veut trouver la valeur de x qui maximiserait la contenance de sa goutti`ere.
2. Montrer que V (x) = −1200(x − 3, 5)2 + 14700.
-
@cestmoilesgars Bonsoir,
Exprime en fonction de xxx, chacune des dimensions de la gouttière.
-
mtschoon dernière édition par

Bonjour,
@cestmoilesgars , un schéma :
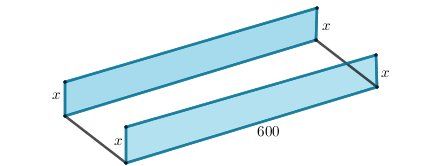
Les rectangles en bleu sont les zones relevées.
Condition : 2x<142x\lt 142x<14 <=> x<7x\lt 7x<7
En centimes :
longueur=600600600
largeur=14−2x14-2x14−2x
hauteur=xxxEn cm3cm^3cm3 :
V(xV(xV(x)=longueur x largeur x hauteur=600×(14−2x)×x600\times (14-2x)\times x600×(14−2x)×xEssaie de poursuivre.
Reposte si besoin.
-
Ccestmoilesgars dernière édition par
@mtschoon
C’est bon merci j’ai développé et j’ai trouvé -1200x au carré + 8400x - 14700
-
mtschoon dernière édition par

@cestmoilesgars , recompte
L'expression que tu donnes n'est pas exacte.
-
mtschoon dernière édition par

Je te fais le calcul :
V(x)=(8400−1200x)×x=8400x−1200x2V(x)=(8400-1200x)\times x=8400x-1200x^2V(x)=(8400−1200x)×x=8400x−1200x2
Il te reste à vérifier que :
8400x−1200x2=−1200(x−3.5)2+147008400x-1200x^2=-1200(x-3.5)^2+147008400x−1200x2=−1200(x−3.5)2+14700$