Exercice symétrie de deux points par rapport à une droite

[Antonin]

Bonjour,
J'ai besoin de votre aide car je n'arrive pas à démontrer cet exercice.
Montrer que les points M(x;f(x)) et M'(x;f1(x)) avec f1(x)= e^x/e^x(1+e^x) et f(x)=1/1+e^x sont symétriques par rapport à la droite d'équation y=1/2
Je dois ensuite dire comment j'obtiens la courbe Cf1 à partir de la courbe Cf

Merci pour votre aide (c'est un peu urgent s'il vous plaît)

[Antonin]

J'ai oublié de préciser mais c'est pour tout réel x

[Wilmat]

Bonjour,

es-tu sûr des expressions de f1(x) et f2(x) car il doit manquer des parenthèses

de plus, $\frac{e^x}{e^x}=1$

[Black-Jack]

@Antonin a dit dans Exercice symétrie de deux points par rapport à une droite :

Bonjour,
J'ai besoin de votre aide car je n'arrive pas à démontrer cet exercice.
Montrer que les points M(x;f(x)) et M'(x;f1(x)) avec f1(x)= e^x/e^x(1+e^x) et f(x)=1/1+e^x sont symétriques par rapport à la droite d'équation y=1/2
Je dois ensuite dire comment j'obtiens la courbe Cf1 à partir de la courbe Cf

Merci pour votre aide (c'est un peu urgent s'il vous plaît)

Bonjour,

Je parierais que ce que tu as essayé d'écrire (mais c'est raté) était :

$f_1(x)=\frac{e^x}{1+e^x}$
et
$f(x)=\frac{1}{1+e^x}$

[mtschoon]

Bonjour,

Oui.
En prenant :
$f(x)=\frac{1}{1+e^x}$ . Courbe $(C_f)$
$y=\frac{1}{2}$ . Droite $(D)$
On obtient, en cherchant l'équation de la courbe
$(C_{f_1})$ symétrique de $(C_f)$ par rapport à $(D)$ :
$f_1(x)=\frac{e^x}{1+e^x}$

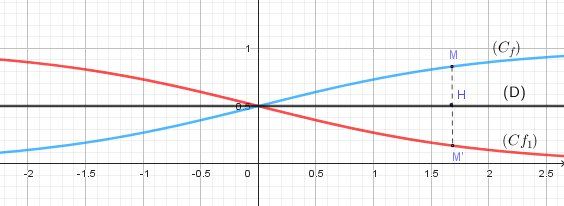
Reste à @Antonin à démontrer, par exemple, que $(D)$ est la médiatrice de $[M{M}^{\prime }]$

[Black-Jack]

Bonjour,

Je ne sais pas ce qui est enseigné actuellement.

... mais il me semble qu'un simple regard aux expressions données (les correctes) de f1(x) et f(x), permet de voir que pour tout x de R, on a f1(x) + f(x) = 1, et donc ...

[mtschoon]

@Black-Jack , bonjour,

Idem pour moi.
Je ne sais pas précisément la méthode qui est vue en cours de Terminale actuellement (c'est ça la retraite ! ...) et les programmes changent fréquemment.
C'est pour cela que j'ai noté "par exemple"dans mon message.

Si @Antonin passe voir les réponses, peut-être qu'il le dira.

Vu que @Antonin à indiquer "Montrer que les points M(x;f(x)) et M'(x;f1(x)) " sont symétriques par rapport à la droite d'équation y=1/2, je lui ai répondu par la médiatrice à utiliser.