Ensemble de définition
-
MMMounah dernière édition par Noemi
Bonsoir,
Svp c’est quoi l’ensemble de définition de f(x)=x+1x−1f(x) = \sqrt{\dfrac{x+1}{x-1}}f(x)=x−1x+1Expression de la fonction écrite en Latex par la modération du site.
-
@Zeïnab-Mahamadou Bonsoir,
Fais un tableau de signes :
xxx
x+1x+1x+1
x−1x-1x−1
f(x)f(x)f(x)
-
LLunasweet dernière édition par Casebas
Salut,
L'ensemble de définition de la racine carrée de [(x+1)/(x-1)] est l'ensemble des valeurs de x pour lesquelles l'expression sous la racine est positive. Il faut donc résoudre l'inéquation [(x+1)/(x-1)] > 0. Pour cela, on peut utiliser le signe du quotient de deux fonctions, en étudiant le signe du numérateur (x+1) et du dénominateur (x-1). On obtient le tableau de signes suivant :
x | -∞ | -1 | 1 | +∞
(x+1) | - | 0 | + | +
(x-1) | - | - | 0 | +
[(x+1)/(x-1)] | + | 0 | - | 0 | +On voit que l'expression est positive quand x < -1 ou x > 1. Donc l'ensemble de définition est ]-∞ ; -1 ∪ ]1 ; +∞[. Tu peux trouver plus d'explications sur ce site : Ensemble de définition de la racine carrée d’ une fonction : piger-lesmaths. fr/ensemble-de-definition-de-la-racine-carree-d-une-fonction. J'espère que ça t'aide.
-
mtschoon dernière édition par mtschoon

Bonjour,
Je donne quelques précisions dans cette étude.La condition d'existence du quotient x+1x−1\dfrac{x+1}{x-1}x−1x+1 est x≠1\boxed{x\ne 1}x=1 (car on ne peut pas diviser par 0)
Il faut donc mettre une double barre dans le tableau de signes.De plus, la condition d'existence de x+1x−1\sqrt{\dfrac{x+1}{x-1}}x−1x+1 est x+1x−1≥0\boxed{\dfrac{x+1}{x-1}\ge 0}x−1x+1≥0 (on peut prendre la racine carrée d'un nombre strictement positif ou nul)
Le tableau de signes est donc ainsi :
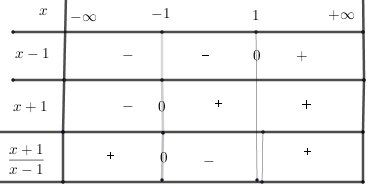
L'ensemble de défintion de la fonction fff définie par f(x)=x+1x−1f(x)=\sqrt{\dfrac{x+1}{x-1}}f(x)=x−1x+1 est donc :
Df=]−∞,−1]∪]1,+∞[\boxed{D_f=]-\infty,-1] \cup ]1,+\infty[}Df=]−∞,−1]∪]1,+∞[ (faire bien attention aux crochets)Bon travail !
-
BBlack-Jack dernière édition par
@mtschoon a dit dans Ensemble de définition :
Bonjour,
Je remarque quelques incorrections dans la réponse ci-dessus.La condition d'existence du quotient x−1x+1\dfrac{x-1}{x+1}x+1x−1 est x≠−1\boxed{x\ne -1}x=−1 (car on ne peut pas diviser par 0)
Il faut donc mettre une double barre dans le tableau de signes.De plus, la condition d'existence de x−1x+1\sqrt{\dfrac{x-1}{x+1}}x+1x−1 est x−1x+1≥0\boxed{\dfrac{x-1}{x+1}\ge 0}x+1x−1≥0 (on peut prendre la racine carrée d'un nombre strictement positif ou nul)
Le tableau de signes est donc ainsi :
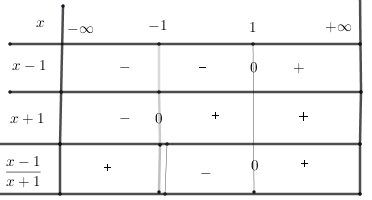
L'ensemble de défintion de la fonction fff définie par f(x)=x−1x+1f(x)=\sqrt{\dfrac{x-1}{x+1}}f(x)=x+1x−1 est donc :
Df=]−∞,−1[∪[1,+∞[\boxed{D_f=]-\infty,-1[ \cup [1,+\infty[}Df=]−∞,−1[∪[1,+∞[ (faire bien attention aux crochets)Bon travail !
Bonjour,
Juste une petite remarque.
Le quotient était x+1x−1\frac{x+1}{x-1}x−1x+1 et pas x−1x+1\frac{x-1}{x+1}x+1x−1
-
mtschoon dernière édition par

@Black-Jack , bonjour,
Merci pour ta relecture d'énoncé.
J'ai modifié ma réponse avec f(x)=x+1x−1f(x)=\sqrt{\dfrac {x+1}{x-1}}f(x)=x−1x+1