aire d'un disque et angle

[Marvin]

Bonjour j'envoi cet exercice particulier car je dois préparer un oral et à vrai dire et honnêtement j'ai rien compris dans cet exo.
Voici mes tentatives de réponses :Concernant l'exo ce que j'ai pû dire pour l'instant c'est que:
Aire disque= aire cercle =pir²
La mesure en radian varie sur ]0;pi] donc l'angle alpha est inférieur a 180 degré (pi).
Aire de la surface quadrillée = Basehauteur/2 =B*1/2 puisque h=rayon =1. et puisque la base c'est BC, alors l'aire est BC/2.

Quelqu'un pourra-t-il le corrigé svp? (et/ou donner son avis sur les productions d'élèves svp)

L'exercice:
Url image :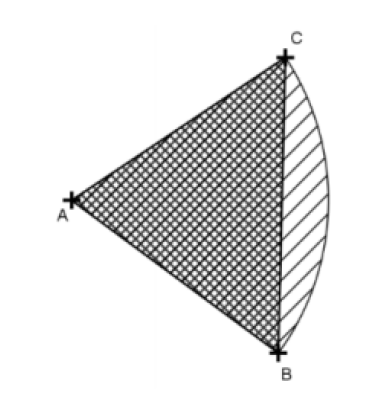
https://ibb.co/6wVxv2z
La figure ci-contre représente une portion d'un disque de centre $A$ et de rayon 1. On fait varier la mesure en radian de l'angle $\widehat{BAC}$ dans l'intervalle $]0;\pi ]$.
Déterminer un encadrement d'amplitude $10^{-3}$ d'une mesure de l'angle $\widehat{BAC}$ pour laquelle il y a égalité des aires de la surface hachurée et de la surface quadrillée.
Adapté du manuel Maths'x terminale S spécifique programme 2012
Réponses de trois élèves de classe de terminale spécialité mathématiques
Élève 1
J'ai posé $\widehat{BAC}=\alpha$ donc l'aire de $ABC=\frac{B\times h}{2}=\sin \left(\frac{\alpha }{2}\right)\cos \left(\frac{\alpha }{2}\right)$.
L'aire du secteur hachuré est égale à l'aire de la portion de disque privé de l'aìre du triangle ABC.
Je résous l'équation
$\frac{\alpha }{2}-\sin \left(\frac{\alpha }{2}\right)\cos \left(\frac{\alpha }{2}\right)=\sin \left(\frac{\alpha }{2}\right)\cos \left(\frac{\alpha }{2}\right)$.
Je pose $f(\alpha )=2\sin \left(\frac{\alpha }{2}\right)\cos \left(\frac{\alpha }{2}\right)-\frac{\alpha }{2}$.
Avec ma calculatrice graphique, je trouve une solution entre $\frac{\pi }{2}$ et $\pi$.
Jai écrit un programme en langage python.
Il retourne $a=3,14082566319585$
et $b=3,141592653589793$.
from math import sin, cos, pi def $f(x)$ :
return $2\ast \sin (x/2)\ast \cos (x/2)-x/2$
def dicho():
$a=pi/2$
$b=pi$
while b-a>=0.001 :
$m=(a+b)/2$
if f(m)<0 :
$a=m$
else
$b=$
return $a,b$

Élève 2
J'ai posé $x=\frac{\widehat{BAC}}{2}$ donc l'aire de $ABC$ est $\sin (x)\cos (x)$ et l'aire du secteur hachuré $x-\sin (x)\cos (x)$.
Je résous l'équation $x-2\sin (x)\cos (x)=0$.
J'étudie la fonction $f$ définie par :
$f(x)=x-2\sin (x)\cos (x)=x-\sin (2x)$ donc
$f^{\prime }(x)=1-\cos (2x)$.
Comme la dérivée est positive, $f$ est strictement croissante.
D'après le théorème de bijection il y a une unique solution.

Le travail à exposer
1- Analysez les productions de ces deux élèves en mettant en évidence les compétences acquises, les erreurs éventuelles ainsi que l'aide que vous pourriez leur apporter.
2- Proposez une correction de l'exercice telle que vous la présenteriez devant une classe de première spécialité mathématiques, en vous appuyant sur les productions des élèves.

[Noemi]

@Marvin Bonjour,

Pour les relations, regarde ce lien : http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Secteur.htm

Pour les productions des élèves, indique tes remarques.
Ont-ils répondu à la question posée ?

[Marvin]

Hello merci beaucoup pour ton aide.
Si j'ai bien compris, l'angle BAC = alpha (que j'appel k pour écrire facilement).
du cours on doit avoir 1/2.R²sink=1/2.R²(k-sink).
d'ou sink= k -sink, ce qui implique k= 2sink (alpha= 2sin alpha). Je n'ai pas l'impression que les élèves ont répondu a la question

[Noemi]

@Marvin

Tu ne réponds pas aussi à la question.
De plus, il faut analyser les productions des deux élèves.

[Marvin]

sin alpha/alpha =1/2 bin oui j'ai oublié ça merci!

[Black-Jack]

@Marvin a dit dans aire d'un disque et angle :

sin alpha/alpha =1/2 bin oui j'ai oublié ça merci!

Bonjour,

Non, tu n'as pas fini.

Tu n'as pas fait ceci (qui est demandé dans l'énoncé)

"Déterminer un encadrement d'amplitude $10^{-3}$ d'une mesure de l'angle $\widehat{BAC}$ pour laquelle il y a égalité des aires de la surface hachurée et de la surface quadrillée."

Tu DOIS montrer qu'une seule valeur d'angle convient et en déterminer la valeur (avec la précision demandée)

Et tu n'as pas non plus répondu à "donner son avis sur les productions d'élèves"

Bien que là, ce n'est pas clair si il faut ou non obligatoirement le faire ... si on a résolu l'exercice en entier.
A cause du "et/ou" de la phrase : (et/ou donner son avis sur les productions d'élèves svp)

[Marvin]

Ah ok merci, les production d'élève j'ai donné un avis sur ma feuiller j'ai pas taper ici, ok ok merci beaucoup

[Marvin]

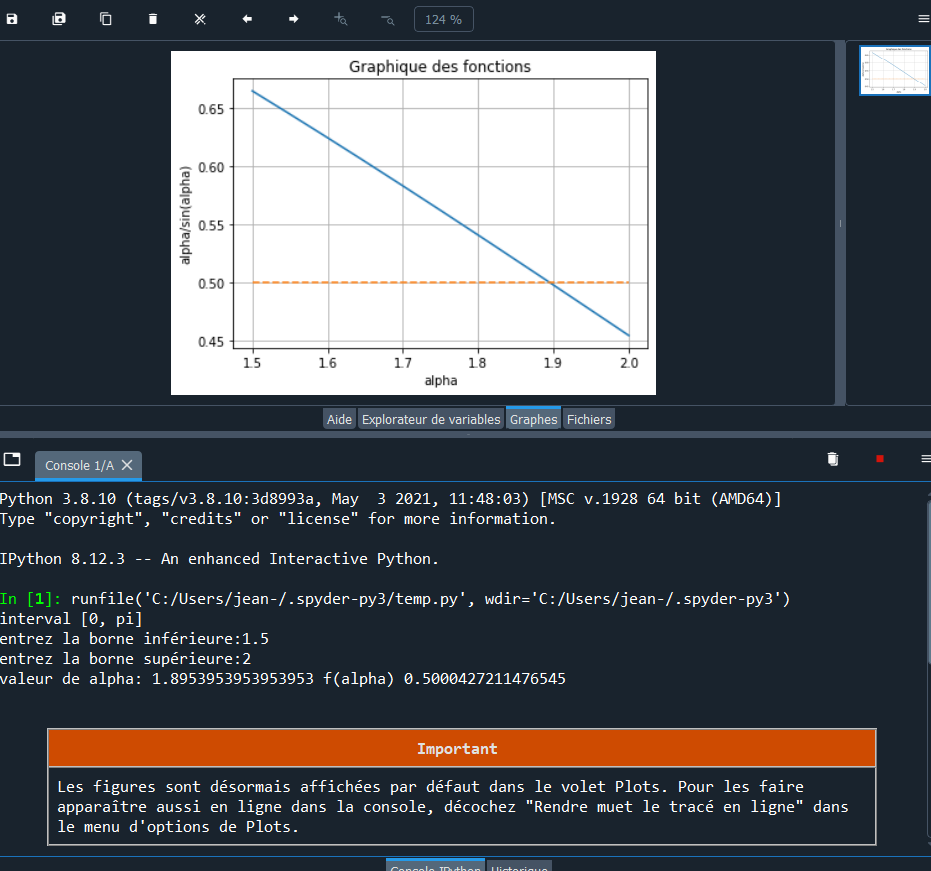
Ça affiche la courbe de la fonction sin(x)/x et la droite de constante 1/2. On peut voir le point de croisement entre les 2. Et à l'aide d'une boucle for j'estime le point x le plus proche pour lequel f(x) = 1/2.