Question récurrence matrice
-
Nastog dernière édition par
Soit A=
0 2 -1
0 0 3
0 0 1- Montrer que A3 = A2.
- Montrer par récurrence que pour tout entier naturel
n=>2, A°=A2.
Je ne sais pas quoi mettre dans mon initialisation, si je dois mettre les matrices ou juste A et pour l’hérédité je ne sais pas si cela est juste, je n’ai rien rédigé mais je connais les phrases à mettre :
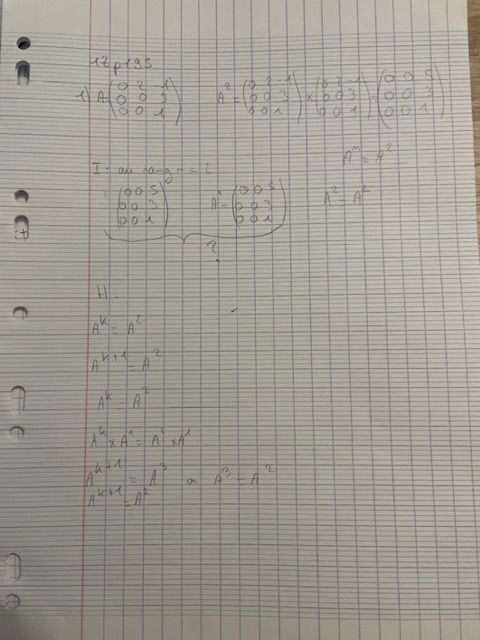
-
mtschoon dernière édition par

@Nastog , bonjour,
A la première question, tu as dû démontrer que : A3=A2A^3=A^2A3=A2
Tu peux t'en servir pour la récurrence , c'est l'interét de la question.S'il s'agit bien de n≥2n\ge 2n≥2, l'initialisation est pour n=2n=2n=2
L'initialisation est donc trivial : A2=A2A^2=A^2A2=A2Pour l'hérédité :
Tu supposes pour pour un ordre k≥2k\ge 2k≥2 : Ak=A2A^k=A^2Ak=A2
Tu dois prouver que Ak+1=A2A^{k+1}=A^2Ak+1=A2
Démonstration :
Ak+1=Ak×A1=Ak×AA^{k+1}=A^k\times A^1=A^k\times AAk+1=Ak×A1=Ak×A
Par hypothèse de la récurrence,Ak=A2A^k=A^2Ak=A2 donc :
Ak+1=A2×A=A3A^{k+1}=A^2\times A=A^3Ak+1=A2×A=A3Vu qu'à la première question tu as prouvé que A3=A2A^3=A^2A3=A2, tu obtiens :
Ak+1=A2A^{k+1}=A^2Ak+1=A2CQFD.
-
Nastog dernière édition par Noemi
@mtschoon
D’accord merci beaucoup j’ai compris, j’en profite pour poser une deuxième question sur un autre exo mais toujours de la récurrence :
Enfaite j’ai encore un problème pour l’initialisation ( décidément..) la deuxième photo est la correction de l’exercice et moi j’ai fais ça :

J’aimerais donc savoir si ce que j’ai fais convient et sinon ou est mon erreur
Scan de l'énoncé supprimé par la modération du site.
-
@Nastog Bonsoir,
Attention, tu ne respectes pas le réglement du forum.
Le scan ou un lien de l'énoncé de l'exercice est interdit sur ce forum. Seuls les scans de schémas, graphiques ou figures sont autorisés.Le scan va être supprimé par la modération du site.
-
mtschoon dernière édition par

@Nastog ,
c'est parfait si tu as compris ton exercice.Par contre, il faut ouvrir une seconde discussion pour un second exercice.
En plus, la modération te dira qu'ici , les scans d'énoncés ne sont pas autorisés.
Il faudra donc ouvrir une autre discussion et écrire l'énoncé.
-
mtschoon dernière édition par

Bonsoir @Noemi
Je n'avais pas vu tes remarques , sinon je ne les aurais pas faites...!
-
Nastog dernière édition par
Ahhh d’accord c’est la première j’utilise ce site et j’avoue ne jamais lire les règles
 Désolé pour la gêne occasionnée. Je vais réouvrir un salon.
Désolé pour la gêne occasionnée. Je vais réouvrir un salon.
-
mtschoon dernière édition par

@Nastog , bonjour,
OK.
Ouvre une nouvelle discussion et écrivant l'énoncé, si tu as besoin.