Rapports trigonométriques

[galois]

Salut et merci d'avance de m'aider pour la 2ème question.

ACD est rectangle en A tel que : CD=1 et l'angle en D égale à 15°.
B le point de [AD] tel que AB = AC.
On pose AB= x et BD=y
1)Exprimer cos(15°) en fonction de x et y
(J'ai trouvé x +y)
2)Déduire que: cos(45°) +cos(75°) = cos(15°)

[Noemi]

@galois Bonjour,

une piste : Utilise une relation trigonométrique dans le triangle $BCD$.

[mtschoon]

Bonjour,

@galois , un schéma si besoin pour t'éclairer

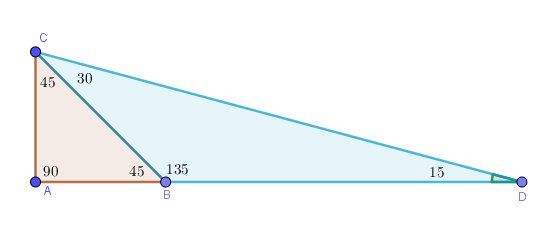
OK pour $cos(15°)=x+y$

$cos(75°)=\frac{AC}{CD}=AB=x$

Comme te le dit @Noemi , tu peux utiliser le triangle $BCD$
Par exemple, avec la loi de sinus, si tu connais, tu peux obtenir:
$\frac{1}{sin(135°)}=\frac{y}{sin(30°)}$

Avec les angles remarquables, tu exprimes $sin(135°)$ et $sin(30°)$

Tu pourrais déduire $y=\frac{\sqrt{2}}{2}=cos(45°)$ et terminer ta question.

Bons calculs.

[galois]

@mtschoon merci mais
on connaît uniquement les rapports trigonométriques d'un angle aigu.

[mtschoon]

@galois , bonjour,

Si tu connais les rapports trigonométriques des angles aigus remarquables, tu peux en déduire les rapports trigonométriques de l'angle de 135°.
(angles supplémentaires)
Représente les angles sur le cercle trigonométrique éventuellement.

$sin(135°)=sin(180°-45°)=sin(45°)=\frac{\sqrt{2}}{2}$

[galois]

@mtschoon excusez moi mais l'exercice porte sur les angles aigus dans un triangle rectangle uniquement

[galois]

@galois voilà j'ai trouvé
Il suffit de faire le projeté orthogonal Hde B sur (CD) puis on calcule BH de deux manières on trouve sin15 = x
Merci

[mtschoon]

@galois , bonjour,

Ton énoncé de départ ne précisait pas il fallait utiliser exclusivement des angles aigus.
La méthode la plus simple t'a donc était donnée.

Si tu as trouvé une méthode correspondant à cette contrainte (angles aigus), c'est parfait !

Cette question ( prouver que cos(45°) +cos(75°) = cos(15°) ) est un classique.
Pour lecture, je te mets un lien où quelques méthodes sont utilisées.

https://www.cut-the-knot.org/m/Geometry/cos75_cos45_cos15.shtml
Bon travail !

[Black-Jack]

Bonjour,

Juste pour info.

Par manipulation de relations trigonométriques simples et avec la connaissance des valeurs des sin et cos des valeurs caractéristiques, on peut aussi trouver les valeurs de cos(15°) et cos(75°)

Par exemple (autres autres méthodes) :

cos(2x) = 2cos²(x)-1
cos(30°) = 2.cos²(15°)-1
$\frac{\sqrt{3}}{2}=2.co{s}^2(15^o)-1$
$co{s}^2(15^o)=\frac{1+\frac{\sqrt{3}}{2}}{2}=\frac{2+\sqrt{3}}{4}$
et comme 15° est dans le 1er quadrant : $cos(15^o)=\frac{\sqrt{2+\sqrt{3}}}{2}$
cos(75°) = sin(15°) car ...
cos²(75°) = sin²(15°) = 1 - cos²(15°)
$co{s}^2(75°)=1-\frac{2+\sqrt{3}}{4}=\frac{2-\sqrt{3}}{4}$
et comme 15° est dans le 1er quadrant : $cos(75°)=\frac{\sqrt{2-\sqrt{3}}}{2}$