Exercice sur le barycentre lieu géométrique urgent

J'aurais besoin d'un coup de main pour cet exo qui me pose vraiment probléme!
Voila l'énoncé:
ABC est un triangle, k est un réel quelconque.
1° A quelle condition le barycentre de (A; k-4), (B; 2k-4) et (C; 3k+2) existe t-il?
2° On appelle Gk (k en indice) le barycentre de (A; k-4), (B; 2k-4) et (C; 3k+2) lorsqu'il existe.
Quel est le lieu géométrique des points Gk lorsque k varie dans R{1}?
Merci d’avance pour l’aide ………………………………………. ……

@Malak-Laabous Bonsoir, (marque de politesse à ne pas oublier !!)

La première question est une question de cours.
Analyse la réponse donnée ici : https://forum.mathforu.com/topic/8749/déterminer-si-le-barycentre-existe-et-son-lieu-géométrique

Ce message a été supprimé !

@Malak-Laabous

Tu dois utiliser deux barycentres, le point $G_0$ pour $k = 0$ et un point $H$ par exemple pour le barycentre des points $A (1)$ , $B (2)$ et $C (3)$ .
Puis utiliser les relations vectorielles.

Ces éléments étaient peut-être indiqués dans l'énoncé.

@Malak-Laabous

$AG0→=16(4AB→−2AC→)\overrightarrow{AG_{0}}=\dfrac{1}{6}(4\overrightarrow{AB}-2\overrightarrow{AC})$

@Noemi alors comment est ce que je peux rédiger une réponse convenable? Merci pour votre temps

@Malak-Laabous

Avec
$AH→=16(2AB→+3AC→)\overrightarrow{AH}=\dfrac{1}{6}(2\overrightarrow{AB}+3\overrightarrow{AC})$
Cherche une relation entre $HGK→\overrightarrow{HG_K}$ et $HG0→\overrightarrow{HG_0}$ .

Ce message a été supprimé !

@Malak-Laabous

Quelle relation as-tu trouvée ?

Ce message a été supprimé !

Bonjour,

Seulement une info,

Je n'ai fait aucun calcul !
J'ai seulement vu que cet énoncé est le numéro 41 ici :
https://download.tuxfamily.org/mathsp/Bases/PDF-1ereS/barycentre.pdf

Il y a le schéma et l'indication :

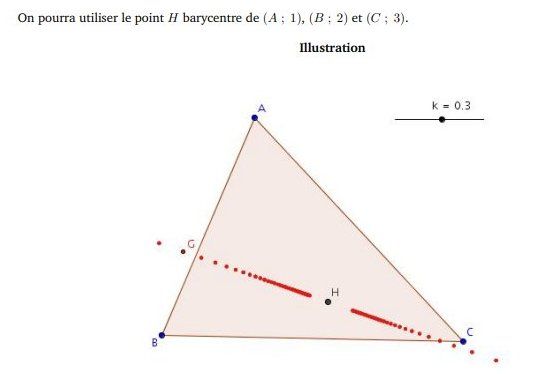
Cela donne une idée de la conclusion à trouver.

@Malak-Laabous
A partir de
$AGk→=16−6k[(4−2k)AB→−(2+3k)AC→]\overrightarrow{AG_k}=\dfrac{1}{6-6k}[(4-2k)\overrightarrow{AB}-(2+3k)\overrightarrow{AC}]$
que tu peux écrire :
$(6−6k)AGk→=(4−2k)AB→−(2+3k)AC→(6-6k)\overrightarrow{AG_k}=(4-2k)\overrightarrow{AB}-(2+3k)\overrightarrow{AC}$
Tu déduis
$AG0→=16[4AB→−2AC→]\overrightarrow{AG_0}=\dfrac{1}{6}[4\overrightarrow{AB}-2\overrightarrow{AC}]$
ou
$6AG0→=4AB→−2AC→6\overrightarrow{AG_0}=4\overrightarrow{AB}-2\overrightarrow{AC}$

Avec le point $H$
$AH→=16(2AB→+3AC→)\overrightarrow{AH}=\dfrac{1}{6}(2\overrightarrow{AB}+3\overrightarrow{AC})$
soit
$6AH→=2AB→+3AC→6\overrightarrow{AH}=2\overrightarrow{AB}+3\overrightarrow{AC}$

Tu en déduis :
$(6−6k)AGk→=6AG0→−6kAH→(6-6k)\overrightarrow{AG_k}=6\overrightarrow{AG_0}-6k\overrightarrow{AH}$
On trouve $G0GK→=kHGk→\overrightarrow{G_0G_K}=k\overrightarrow{HG_k}$ .
D'ou la conclusion : ...

Ce message a été supprimé !

Pas géné "Malak-Laabous" devenu "Ancien Utilisateur" après avoir supprimé l'énoncé et tout ce qu'il a écrit...!

Pour le cas où ce topic resterait(? ? ? ), je recopie l'énoncé 41 du lien pour que des lecteurs éventuels puissent comprendre.

ABC est un triangle.
k est un réel quelconque différent de 1.
On appelle $G_k$ le barycentre de $(A; k - 4), (B; 2 k - 4) e t (C; 3 k + 2)$ .
Quel est le lieu géométrique des points $G_k$ lorsque k prend toutes les valeurs possibles (différentes de 1)?
On pourra utiliser le point H barycentre de $(A; 1), (B; 2) e t (C; 3)$ .