devoir maison dérivation, limite etc
-
Mmath58004 dernière édition par
Bonjour
J'ai un dm à faire, il est simple donc j'ai tous fais sauf une question que je n'ai pas réussi, je ne sais pas le raisonnement qu'il faut avoir, alors j'aimerai de l'aide s'il vous plaît
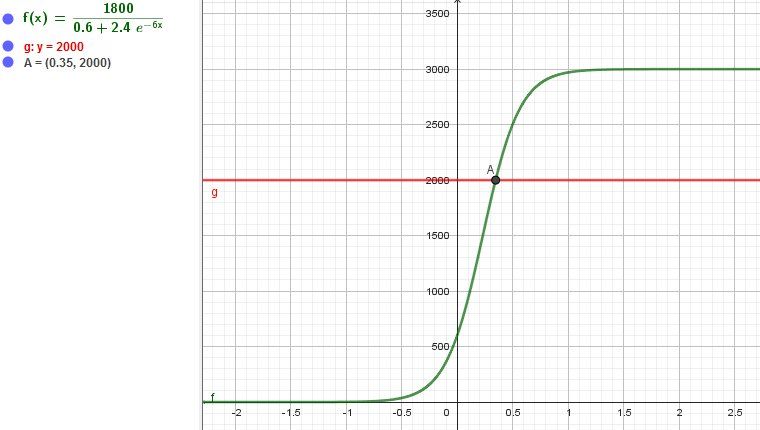
On considère la fonction f(t)=1800/(0,6+2,4∗exp(−6t))f(t)=1800/(0,6+2,4*exp(-6t))f(t)=1800/(0,6+2,4∗exp(−6t))
Après j'ai du faire la dérivée, le tableau de signe/variation, déterminer f(0) et la limite en plus infini, je l'ai fais sans problème
La Q4 : Expliquer pourquoi l'équation f(t)=2000 possède une seule solution. C'est là que je bloque...
-
@math58004 Bonjour,
Utilise le tableau de variations. Comment varie f(t)f(t)f(t) ?
-
Mmath58004 dernière édition par
@Noemi
f est croissante
-
Oui et f(x)f(x)f(x) varie de .... à .... donc d'après le théorème ....
-
Mmath58004 dernière édition par
le théorème des valeurs intermédiaires ? j’y avais pensé mais je sais pas comment l’utiliser
je suppose qu’ici ça varie de moins infini à plus infini
-
lina benazzouz dernière édition par
@Noemi a dit dans devoir maison dérivation, limite etc :
Oui et f(x)f(x)f(x) varie de .... à .... donc d'après le théorème ....
-
mtschoon dernière édition par

Bonjour,
@lina-benazzouz ? ? ?
@math58004 , quelques détails si besoin.
Je suppose que tu as étudié fff surRRR et que tu as trouvé f strictement croissante car dérivée strictement positive.
La limite de f(t)f(t)f(t) en −∞-\infty−∞ et 000 et la limite en +∞+\infty+∞ est 300030003000Tu pourrais appliquer le TVI ( cas de la bijection ) sur tout RRR pour prouver que l'équation f(t)=2000f(t)=2000f(t)=2000 possède une seule solution.
C'est le plus rapide.Voir lien :
https://etablissementbertrandeborn.net/blog/public/document_maths/TVI_et_TB.pdfVu que l'on te demande de calculer f(0)f(0)f(0) tu peux éventuellement l'utiliser.
Pour t<0t\lt 0t<0, f(t)<600f(t)\lt 600f(t)<600 donc sur ]−∞,0[]-\infty,0[]−∞,0[ , f(t)=2000f(t)=2000f(t)=2000 n'a pas de solution.
Pour t≥0t\ge 0t≥0, fff est strictement croissante (donc bijective) et prend des valeurs de 600600600 à 300030003000
Par TVI ( cas de la bijection), il existe une seule valeur de t positive telle que f(t)=2000f(t)=2000f(t)=2000A la calculette, la solution est voisine de 0.3465740.3465740.346574
-
mtschoon dernière édition par

Illustration graphique ( en prenant des unités adaptées)