Géométrie vectorielle
-
MMMounah dernière édition par
Bonsoir
Soit l’application f est définie analytiquement par :
x’= 1/2(¥3x -y -¥3)
Y’=1/2(x +¥3y +2¥3-5)
Nb ¥= racine carré-
Vérifier f admet un unique point invariant 2 dont on calculera les coordonnées.
-
Démontrer que fest bijective et déterminer l'expression analytique de sa réciproque
-
Soient (x, y) et (X, Y) les couples de coordonnées d'un point M dans les repères ( 0 ; vec i ; vec j ) et ( Omega ; vec i ; vec j ) respectivement
Aidez moi avec la question 3 svp
-
-
BBlack-Jack dernière édition par
Bonjour,
Ton écriture d'équation est sujette à interprétation.
Est-ce : x′=12(3.x−y+3)x' = \frac{1}{2} (\sqrt{3}.x - y + \sqrt{3}) x′=21(3.x−y+3)
ou bien : x′=12(3x−y+3)x' = \frac{1}{2} (\sqrt{3x} - y + \sqrt{3}) x′=21(3x−y+3)
ou bien autre chose ?Même confusion possible pour ton y' = ...
-
MMMounah dernière édition par
@Black-Jack Bonsoir
C'est le premier x' qui est correct mais à la fin c'est
-√ 3 et non pas + √ 3
x'= 1/2( √ 3 .x -y -√ 3 )
Et le y'= 1/2( x + (√ 3 )y +(2 √ 3 ) -5)
-
@Zeïnab-Mahamadou Bonsoir,
Il manque des éléments à la question 3.
-
MMMounah dernière édition par
@Noemi
a) Exprimer X et Y en fonction de x et y
b) Déterminer l’expression analytique de f dans le repère (Omega ; vec i ; vec j)
-
mtschoon dernière édition par mtschoon

Bonjour,
@Zeïnab-Mahamadou, je regarde ton énoncé complété.
Je pense que le but est de trouver la nature de la transformation fffJe t'indique quelques pistes/réponses ( il faut tout expliciter, ce que je ne fais pas) que tu as dû trouver aux questions 1 et 2 (que tu dis avoir faites)
Au départ, si j'ai bien lu :
{x′=12(3x−y−3)y′=12(x+3y+23−5)\begin{cases}x'=\dfrac{1}{2}(\sqrt3 x-y-\sqrt 3)\cr y'=\dfrac{1}{2}(x+\sqrt 3 y+2\sqrt 3-5)\end{cases}⎩⎪⎪⎨⎪⎪⎧x′=21(3x−y−3)y′=21(x+3y+23−5)Pour le 1), en faisant x′=xx'=xx′=x et y′=yy'=yy′=y tu as obtenu un système de deux équations à deux inconnues xxx et yyy et après calculs, tu as dû obtenir x=1x=1x=1 y=−2y=-2y=−2
Le point invariant par fff est donc le point Ω\OmegaΩ de coordonnées (1,−2)\boxed{(1,-2)}(1,−2)
(Je l'ai appelé Ω\OmegaΩ, bien que tu ne l'aies pas indiqué, pour que la question 3) ait un sens)Pour la 2), tu as dû transformer le système pour exprimer xxx et yyy en fonction de x′x'x′ et y′y'y′ et tirer les conclusions demandées.
Sauf erreur :
{x=12(3x′+y′−3+4)y=12(−x′+3y′+23−3)\begin{cases}x=\dfrac{1}{2}(\sqrt3 x'+y'-\sqrt 3+4)\cr y=\dfrac{1}{2}(-x'+\sqrt 3 y'+2\sqrt 3-3)\end{cases}⎩⎪⎪⎨⎪⎪⎧x=21(3x′+y′−3+4)y=21(−x′+3y′+23−3)
-
mtschoon dernière édition par mtschoon

@Zeïnab-Mahamadou ,
Pour la 3), tu dois faire un changement d'axes par translation, la nouvelle origine étant le point Ω(1,−2)\Omega(1,-2)Ω(1,−2)
Avec les relations usuelles :
x=1+Y,y=−2+Y,x′=1+X′,y′=−2+Y′x=1+Y, y=-2+Y, x'=1+X', y'=-2+Y'x=1+Y,y=−2+Y,x′=1+X′,y′=−2+Y′Tu remplaces dans les relations de départ, tu calcules, tu simplifies le mieux possible et tu dois arriver , sauf erreur, à:
{X′=12(3X−Y)Y′=12(X+3Y)\begin{cases}X'=\dfrac{1}{2}(\sqrt 3X-Y)\cr Y'=\dfrac{1}{2}(X+\sqrt 3 Y)\end{cases}⎩⎪⎪⎨⎪⎪⎧X′=21(3X−Y)Y′=21(X+3Y)Ensuite, pour déterminer la nature de fff, si j'avais écrit l'énoncé, je demanderais de passer par les nombres complexes ( mais ce n'est pas moi qui est écrit l'énoncé, donc je n'en sais rien...)
Je t'indique une piste possible par les complexes
Soit Z′=X′+iY′Z'=X'+iY'Z′=X′+iY′ etZ=X+iYZ=X+iYZ=X+iY
Sauf erreur, Tu dois trouver après calculs :
X′+iY′=12(3+i)(X+iY)X'+iY'=\dfrac{1}{2}(\sqrt 3+i)(X+iY)X′+iY′=21(3+i)(X+iY)
c'est à dire :
Z′=12(3+i)ZZ'=\dfrac{1}{2}(\sqrt 3+i)ZZ′=21(3+i)ZEn mettant sous forme exponentielle,
12(3+i)=32+12i=eiπ6\dfrac{1}{2}(\sqrt 3+i)=\dfrac{\sqrt 3}{2}+\dfrac{1}{2}i=e^{i\dfrac{\pi}{6}} 21(3+i)=23+21i=ei6π
d'où :
Z′=eiπ6Z\boxed{Z'=e^{i\dfrac{\pi}{6}}Z} Z′=ei6πZ
Tu obtiens ainsi la forme complexe de fff rotation d'angle Ω\OmegaΩ et d'angle π6\dfrac{\pi}{6}6πJe me suis fait plaisir en te présentant cette méthode mais , évidemment, utilise celle que tu as vu en cours (qui peut-être autre..., vu que tu postes en Première...)
Bon travail.
-
mtschoon dernière édition par

Illustration graphique
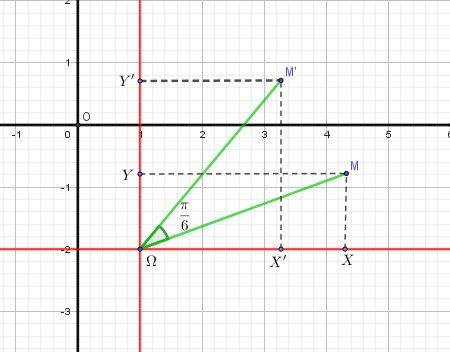
-
MMMounah dernière édition par
@mtschoon
Merci beaucoup monsieur
-
mtschoon dernière édition par

De rien @Zeïnab-Mahamadou , mais ce n'est pas "monsieur", c'est "madame"...
-
medou coulibaly dernière édition par

@mtschoon Bonjour madame comment vous allez ?
-
mtschoon dernière édition par mtschoon

@medou-coulibaly , bonjour,
ça va ,ça va, ...mais... c'est vraiment toi qui poste cet exercice très simple sur "Probabilité de la terminale" alors que tu as le Bac scientifique depuis un ou deux ans (vu que depuis l'an passé, tu postes en Supérieur) ?
C'est bizarre...
Bonne journée.
-
medou coulibaly dernière édition par

@mtschoon
Bonjour madame je voulais faire une revérification avec ce que j'ai fait.merci
-
mtschoon dernière édition par

OK.
Bon week-end @medou-coulibaly
-
medou coulibaly dernière édition par

@mtschoon Madame jusque-là j'ai fait un poste il n'y pas de réponses dessus, sur l'algèbre
-
MMMounah dernière édition par
@mtschoon D’accord c’est noté
Merci madame