Démontrer que 2 droites sont // sans utiliser de repère
-
CChris21300 dernière édition par
Bonjour,
voici le problème du jour

énoncé
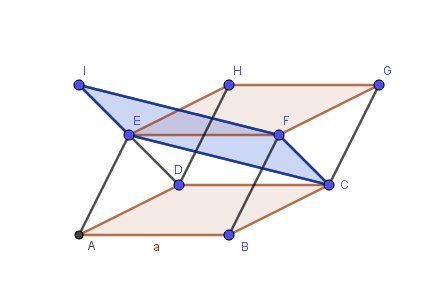
ABCDEFGH est un parallélépipède. I symétrique de D par rapport à E.
- Démontrer que (IF)//(CE) sans utiliser de repère.
- idem en utilisant un repère.
Mes réponses
Pour le 2. aucun problème.
Par contre pour le 1. je n'y parviens pas.Il faut montrer que IF→=kCE→\overrightarrow{IF}=k\overrightarrow{CE}IF=kCE
On sait que IE→=ED→=FC→=1/2ID→\overrightarrow{IE }=\overrightarrow{ED}=\overrightarrow{FC}=1/2\overrightarrow{ID}IE=ED=FC=1/2ID
Je tente de décomposer IF→\overrightarrow{IF}IF afin d'obtenir du CE→\overrightarrow{CE}CE
mais je n'y parviens pas ... Pourriez-vous m'orienter un peu svp ?Merci par avance

-
mtschoon dernière édition par mtschoon

@Chris21300 , bonjour,
Piste à expliciter,
Tu justifies facilement que CF→=DE→\overrightarrow{CF}=\overrightarrow{DE}CF=DE
(diagonales des faces opposées du parallépipède - Tu peux utiliser Chasles pour être rigoureux)Or, DE→=EI→\overrightarrow{DE}=\overrightarrow{EI}DE=EI ( par symétrie de centre E)
Donc CF→=EI→\overrightarrow{CF}=\overrightarrow{EI}CF=EI
Donc CFIECFIECFIE parallélogramme
Donc (IF)//(CE)(IF)//(CE)(IF)//(CE)
-
CChris21300 dernière édition par
Merci @mtschoon pour ton aide !
J'ai grand honte !
En effet, dans ma réponse j'avais bien montré que IE→=FC→\overrightarrow{IE}=\overrightarrow{FC}IE=FC il me suffisait donc d'en déduire que IECF était un parallélogramme et donc que IF→=EC→\overrightarrow{IF}=\overrightarrow{EC}IF=EC et par conséquent que (IF)//(EC) !
Grrr heureusement que la honte ne tue pas sinon je serais déja 3 pieds sous terre
Merci en tout cas @mtschoon

-
mtschoon dernière édition par

Rassure toi @Chris21300 , tu es bien sur terre !
Bonne soirée.