Terminale S , D, C E

[MMounah]

Bonsoir
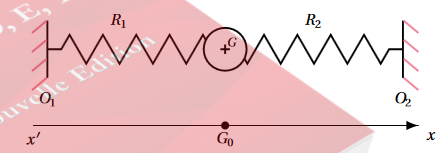
[Un mobile de masse m = 700 g et de rayon R = 5, 0 cm placé sur une table horizontale à coussin d'air est relié à deux ressorts identiques R1 et R2 , comme l'indique la figure ci-dessous. Ces ressorts ont des axes colinéaires horizontaux et ont leurs
extrémités fixées en O_{1} et O_{2}
Ils ont une longueur à vide l_{0}= 20 cm et s'allongent de 4 cm sous l'action d'une force de 1 N. La distance O1O2 est de 70 cm

Comment insérer le schéma du ressort?? Svp

J’écris les questions après la l’image ?

[Noemi]

@Zeïnab-Mahamadou Bonjour,

Pour insérer le schéma, utilise l'icône "mage" et colle le fichier correspondant au schéma.

[MMounah]

@Noemi  ça m’affiche ça et j’arrive pas à coller

[Black-Jack]

C'est ceci ?

[MMounah]

@Black-Jack bonsoir
Oui professeur

[MMounah]

@Black-Jack bonsoir voici les questions
a. Préciser quelle est, à l'équilibre, la position de G, centre d'inertie du mobile. Calculer la valeur Δl de l'allongement de chaque ressort à l'équilibre.
b. On écarte le mobile de sa position d'équilibre de x=5 cm vers O_{1} dans la direction O_{1}O_{2} et on l'abandonne sans vitesse initiale. Il prend alors un mouvement oscillatoire. Montrer en appliquant la deuxième loi de Newton que le mouvement est harmonique. Exprimer et calculer la pulsation et la période du mouvement.
c. Sachant qu'à t = 0 G est à 2 cm de sa position d'équilibre vers O_{2} et se déplace vers O_{1} , donner l'expression qui permet de situer G à chaque instant.

d. Le système (mobile, R_{1} et R_{2} ) est conservatif. Exprimer son énergie mécanique à une date t quelconque et retrouver l'équation différentielle du b

[Noemi]

@Zeïnab-Mahamadou

Tu dois coller le schéma dans la partie (url de l'image).

Regarde les vidéos : https://www.methodephysique.fr/exercices_oscillateurs_harmoniques/#exo2.

Indique tes calculs et/ou résultats si tu souhaites une vérification.

[Black-Jack]

Bonjour,

Je ne suis pas prof.

a)
G est au milieu de [O1O2]
Longueur à l'équilibre pour l'ensemble des 2 ressorts : L = O1O2 - 2R = 70 - 2*5 = 60 cm
Donc donc ressort à une longueur de 1/2 * 60 = 30 cm (0,3m)
L'allongement de chacun des ressorts est alors Delta L = 30 - 20 = 10 cm (0,1 m)

b)
en écartant le mobile de 5 xm vers O1,

Hors position d'équilibre, avec G écarté de la position d'équilibre de la distance x

La force resultante exercée sur la masse m est due au 2 ressorts est est : F = - 2k.x
On a donc la relation : F = m.dx²/dt²
-2kx = m.dx²/dt²

d²x/dt² + (2k/m)*x = 0
avec x(0) = 0,05 (m) et (dx/dt)(0) = 0 (m/s)
avec k = 1/0,04 = 25 N/m la constante d'un ressort

Le mouvement est donc harmonique de pulsation $\omega =\sqrt{\frac{2k}{m}}=\sqrt{\frac{2\ast 25}{0,7}}rad/s$

et $T=\frac{2\pi }{\omega }=...s$

...

c)
Attention, pour cette question, l'énoncé modifie l'instant initial par rapport à la question b.
Cela doit amener à introduire un décalage de phase dans l'expression du mouvement, décalage de phase qu'il faut calculer ...

Continue ... (après avoir vérifié et compris mes calculs)