Terminale terminale terminale
-
MMMounah dernière édition par
Bonsoir
soit a > 0, A, B, C trois points du plan tels que AB = 4a, AC = 3a, BC = 5aDéterminer et construire l'ensemble des points M du plan tels que: MA ^ 2 + MB ^ 2 - 3MC^ 2 = 5a ^ 2
Aider moi svp j’ai trouver $ MG^2 = -6a^2 $ où G est le barycentre des points A B et c…
Soit l’ensemble vide , ce qui est faux je pense comme on a demandé de construire
-
BBlack-Jack dernière édition par Black-Jack
Bonjour,
Méthode parmi d'autre.
On reconnait le triplet Pythagoricien (3a, 4a, 5a) et donc le triangle ABC est rectangle en A.
Dans le repère adéquat, on a : A(0 ; 0), B(4a ; 0) et C(0 ; 3a)
Avec M(X;Y), il vient :
MA² = X²+Y²
MB² = (X-4a)² + Y²
MC² = X² + (Y-3a)²MA² + MB² - 3.MC² = 5a
X²+Y² + (X-4a)² + Y² - 3 * (X² + (Y-3a)²) = 5a²
développer et simplifier -->
X² + Y² + 8aX - 18 aY = -16a²
(X+4a)² + (Y-9²)² = 81a²Le lieu de M est donc (dans le repère décrit), un cercle de centre (-4a ; 9a) et de rayon 9a
-
BBlack-Jack dernière édition par
Rebonjour,
J'ai oublié de joindre le dessin accompagnant ma réponse, le voici :
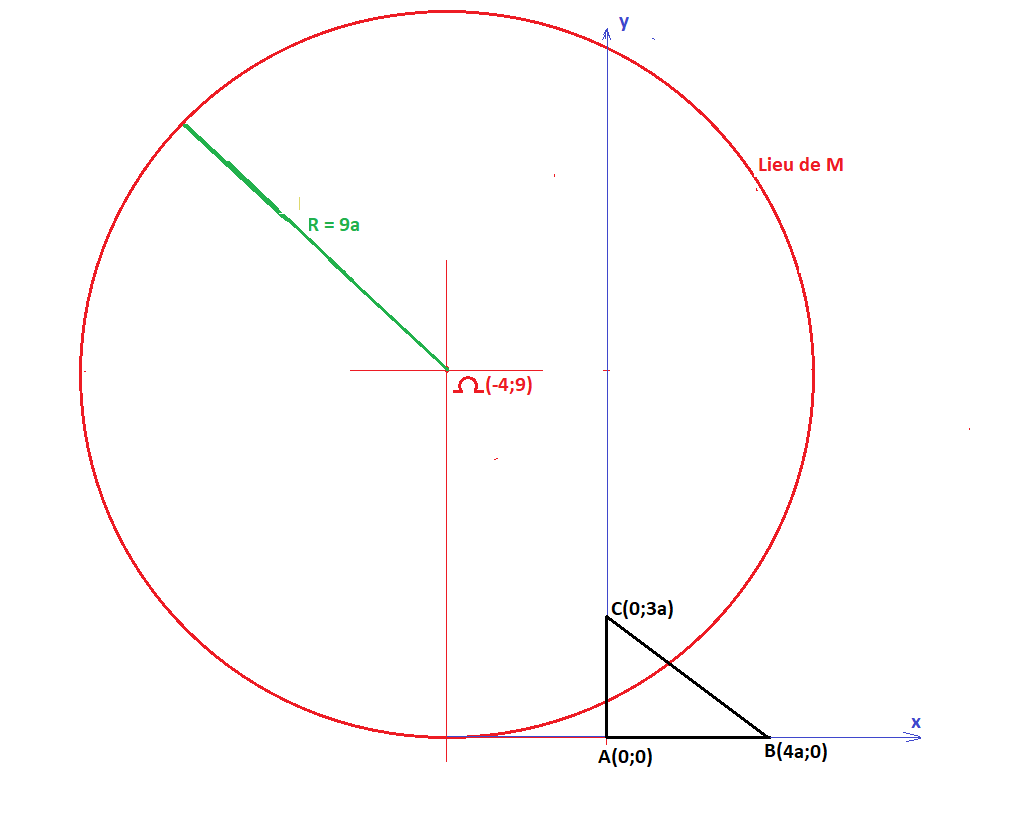
-
MMMounah dernière édition par
@Black-Jack bonsoir
Merci
L’exercice c’est sur le barycentre , vous pouvez y procéder par la méthode de barycentre svp ?
-
MMMounah dernière édition par
@Zeïnab-Mahamadou bonsoir
J’avais fait une erreur de signe à la fin de mon calcul, maintenant que j’ai arranger c’est 6a^2
Ça pourrait être correcte
-
mtschoon dernière édition par mtschoon

Bonjour,
@Zeïnab-Mahamadou a dit dans Terminale terminale terminale :@Black-Jack bonsoir
Merci
L’exercice c’est sur le barycentre , vous pouvez y procéder par la méthode de barycentre svp ?Je t'indique des pistes avec la méthode des barycentres.
GGGest le barycentre de (A,1),(B,1),(C,−3)(A,1),(B,1),(C,-3)(A,1),(B,1),(C,−3)
Avec la propriété d'associativité des barycentres, GGG est le barycentre de (I,2),(C,−3)(I,2),(C,-3)(I,2),(C,−3) en appelant I le milieu de [AB][AB][AB]
En utilisant ton cours, tu trouveras :
IG→=3IC→\overrightarrow{IG}=3\overrightarrow{IC}IG=3ICTu transformes la relation de l'énoncé avec la formule de Leibniz (voir cours)
MA2+MB2−3MC3=(1+1−3)MG2+GA2+GB2−3GC2MA^2+MB^2-3MC^3=(1+1-3)MG^2+GA^2+GB^2-3GC^2MA2+MB2−3MC3=(1+1−3)MG2+GA2+GB2−3GC2
D'où :
−MG2+GA2+GB2−3GC2=5a2-MG^2+GA^2+GB^2-3GC^2=5a^2−MG2+GA2+GB2−3GC2=5a2
Après transformation, tu obtiens :
MG2=−5a2+GA2+BG2−3GC2MG^2=-5a^2+GA^2+BG^2-3GC^2MG2=−5a2+GA2+BG2−3GC2
Il te reste à calculer GA2,GB2,GC2GA^2,GB^2,GC^2GA2,GB2,GC2 en fonction de aaa
-
mtschoon dernière édition par mtschoon

Pour cela , tu peux compléter le schéma en plaçant les points DDD et EEE pour former un rectangle et calculer avec le théorème de Pythagore dans des triangles rectangles.
Je t'indique ce que j'ai trouvé :
GA2=97a2GA ^2=97a^2GA2=97a2
GB2=145a2GB^2=145a^2GB2=145a2
GC2=52a2GC^2=52a^2GC2=52a2Ainsi :
MG2=−5a2+97a2+145a2−156a2MG^2=-5a^2+97a^2+145a^2-156a^2MG2=−5a2+97a2+145a2−156a2
MG2=81a2MG^2=81a^2MG2=81a2
MG=9a\boxed{MG=9a}MG=9a
L'ensemble des points M est le cercle de centre GGG et de rayon 9a9a9a (à tracer dans le schéma).
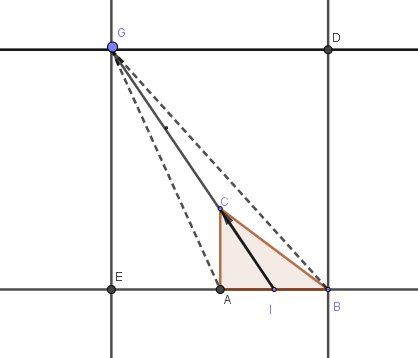
Bons calculs.
-
MMMounah dernière édition par
@mtschoon bonsoir
Merci beaucoup
Je m’étais trompé sur BG^2 j’ai trouvé 70 au lieu de 145 je vais revoir mes calculs
-
MMMounah dernière édition par MMounah
@mtschoon comment je fais pour construire le point G
Je vais essayer de le construire le temps que vous me répondez
-
@Zeïnab-Mahamadou Bonjour,
Pour construire le point GGG utilise la relation : IG→=3IC→\overrightarrow{IG}=3\overrightarrow{IC}IG=3IC
-
mtschoon dernière édition par

@Zeïnab-Mahamadou , j'espère que tu as trouvé maintenant tous les éléments qui te posaient problème.
Bon travail.
-
MMMounah dernière édition par
@mtschoon ouiii merci beaucoup
En plus on nous a amené le même exercice en devoir ce matin
-
mtschoon dernière édition par

Ravie que tu aies bien compris ce DM @Zeïnab-Mahamadou
Tu as fait du bon travail.
J'espère que ton devoir de ce matin s'est bien passé .