équation différentielle

[-lala-o]

Bonsoir,
Je ne comprends pas comment trouver la solution générale dans l'exercice joint ci-dessous (partie que j'ai annotée en bleu sur l'image).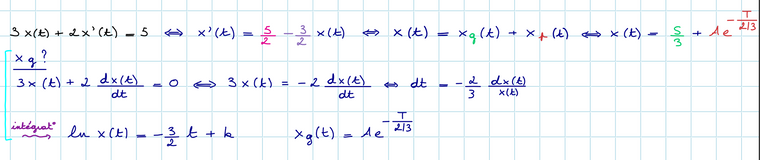

[Noemi]

@lala-o Bonjour,

Attention, l'énoncé de l'exercice est à écrire.
Regarde cette vidéo : https://www.youtube.com/watch?v=CFZr44vny3w
Reprends le calcul en utilisant les explications.

[Black-Jack]

Bonjour,

La 1ère méthode (habituelle) est expliquée dans le lien.

Si tu veux des explications sur une 2 ème méthode (qui démontre tout), alors lis ce qui suit :

3x + 2x' = 5
2x' = 5 - 3x
2.dx/dt = 5-3x
2 dx/(5-3x) = dt
dx/(5-3x) = (1/2) dt

On intègre :

(-1/3) * ln|(5-3x)| = (1/2).t + C (avec C une constante)
ln|(5-3x)| = -3t/2 - 3C
5-3x = e^( -3t/2 - 3C)
5-3x = e^(-3t/2) * e^(-3C)
3x = 5 - e^(-3t/2) * e^(-3C)
x = (5/3) - e^(-3t/2) * (e^(-3C))/3

Et en posant (e^(-3C))/3 = -A (constante), il vient :
x = (5/3) + A.e^(-3t/2)
ou si on préfère : x(t) = (5/3) + A*e^(-t/(2/3))