Logarithmes et fonctions Lambert
-
AArthur24 dernière édition par
Bonjour, j'ai un problème malgré l'utilisation des fonctions Lambert pour résoudre: Xpuissance(X−1)=143Xpuissance(X-1)=143Xpuissance(X−1)=143 quelqu'un aurait-il une idée.
Merci
-
mtschoon dernière édition par

@Arthur24, bonjour,
Trouver les valeurs exactes des solutions me parait mission impossible ( ou presque...?)
Par étude de fonction et TVI, tu dois trouver deux solutions (abscisses de A et B)
xA≈4.36684x_A\approx 4.36684xA≈4.36684
xB≈0.006761x_B\approx 0.006761xB≈0.006761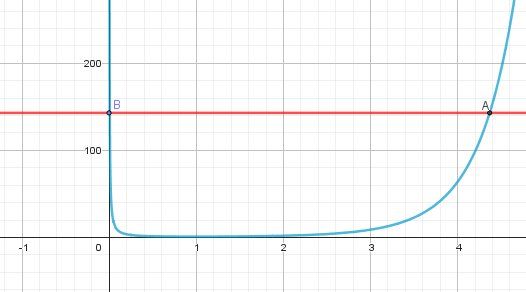
-
AArthur24 dernière édition par
@mtschoon Merci, mais en fait je pensais qu'il était possible de résoudre l'équation sans passer par le graphe en appliquant les formules algébriques du type e^(lnx)=x et W(Ψe^Ψ)=Ψ. Comme par exemple pour résoudre l'équation:
x^x^3=2 voir: https://www.youtube.com/watch?v=Dbs6qhSVU5w
-
mtschoon dernière édition par mtschoon

@Arthur24 , bonsoir,
La méthode que je t'ai indiquée n'est pas graphique.
Le graphique en est que l'illustration.Esprit de Terminale :
Tu étudies la fonction f définie par f(x)=xx−1f(x)=x^{x-1}f(x)=xx−1
Fonction décroissante sur ]0,1]]0,1]]0,1] et croissante sur [1,+∞[[1,+\infty[[1,+∞[
111 n'est pas solution.
Sur chaque intervalle ]0,1]0,1]0,1[ et ]1,+∞[]1,+\infty[]1,+∞[, fff est continue et strictement monotone.
Tu peux utiliser le Théorème des valeurs intermédiaires (cas de la bijection), pour trouver l'existence et l'unicité d'une solution sur chacun de ces deux intervalles.
Et ensuite, calculette, logiciel, ..., te donnent les valeurs approchées avec la précision que tu souhaites.Je n'ai pas cherché si l'utilisation de la fonction de Lambert était pertinente ou non pour cette équation ; peut-être que quelqu'un le fera.
-
AArthur24 dernière édition par
@mtschoon Merci encore, c'est très clair
-
mtschoon dernière édition par

De rien @Arthur24 et bon travail !