Inéquations trigonométriques
-
-lala-o dernière édition par

Bonjour,
J'aimerais avoir une correction pour cet exercice : 2cos2(x)−3sin(x)−22cos^2(x)-\sqrt3 sin(x)-22cos2(x)−3sin(x)−2 < 0
Voici ma réponse : S=U(kϵZ)]−1;−π3+k2π[U]k2π;4π3+k2π[S = U(k\epsilon Z) ]-1;-\frac\pi 3 + k2\pi [ U ]k2\pi ; \frac {4\pi}{3} + k2\pi[S=U(kϵZ)]−1;−3π+k2π[U]k2π;34π+k2π[
-
@lala-o Bonjour,
Même remarque que pour l'autre exercice.
As-tu modifié l'inéquation pour faire apparaitre que la fonction sin(x)sin(x)sin(x) ?
-
BBlack-Jack dernière édition par
@lala-o a dit dans Inéquations trigonométriques :
Bonjour,
J'aimerais avoir une correction pour cet exercice : 2cos2(x)−3sin(x)−22cos^2(x)-\sqrt3 sin(x)-22cos2(x)−3sin(x)−2 < 0
Voici ma réponse : S=U(kϵZ)]−1;−π3+k2π[U]k2π;4π3+k2π[S = U(k\epsilon Z) ]-1;-\frac\pi 3 + k2\pi [ U ]k2\pi ; \frac {4\pi}{3} + k2\pi[S=U(kϵZ)]−1;−3π+k2π[U]k2π;34π+k2π[Bonjour,
Détaille tes calculs.
Je ne trouve pas la même chose.
Pour moi : ]0 ; Pi[ U ]4Pi/3 ; 5Pi/3[ mod 2kPi
-
Tu dois résoudre l'inéquation : 2sin2(x)+3sin(x)>02sin^2(x)+\sqrt3 sin(x) \gt02sin2(x)+3sin(x)>0
Une piste factorise l'expression et fait un tableau de signes.Une vérification graphique avec le graphe de la fonction fff définie par f(x)=2cos2(x)−3sin(x)−2f(x)=2cos^2(x)-\sqrt3sin(x)-2f(x)=2cos2(x)−3sin(x)−2 :
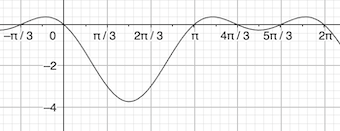
-
mtschoon dernière édition par mtschoon

Bonsoir,
@Noemi a dit dans Inéquations trigonométriques :
Tu dois résoudre l'inéquation : 2sin2(x)+3sin(x)>02sin^2(x)+\sqrt3 sin(x) \gt02sin2(x)+3sin(x)>0
Une piste factorise l'expression et fait un tableau de signes.Une vérification graphique :

@Noemi , pour plus de clarté, ce serait bien d'indiquer l'expression de la fonction dont tu as donné la représentation graphique .
Merci.
-
@mtschoon Bonjour,
C'est la représentation graphique de : f(x)=2cos2(x)−3sin(x)−2f(x)=2cos^2(x)-\sqrt3sin(x)-2f(x)=2cos2(x)−3sin(x)−2 :
et 2cos2(x)−3sin(x)−2=−2sin2(x)−3sin(x)2cos^2(x)-\sqrt3sin(x)-2=-2sin^2(x)-\sqrt3sin(x)2cos2(x)−3sin(x)−2=−2sin2(x)−3sin(x) :
-
mtschoon dernière édition par mtschoon

@Noemi , bonjour,
Merci d'avoir complété par l'expression concernée par le schéma, car il y avait un doute entre 2sin2(x)+(3)sin(x)2sin^2(x)+\sqrt(3)sin(x)2sin2(x)+(3)sin(x) dont tu parlais juste avant et −2sin2(x)−(3)sin(x)-2sin^2(x)-\sqrt(3)sin(x)−2sin2(x)−(3)sin(x)
Maintenant, c'est clair.