Inéquations trigonométrique
-
-lala-o dernière édition par

Bonjour,
J'aimerais avoir une correction pour cet exercice : cos(x)+3sin(x)cos (x) + \sqrt3sin(x) cos(x)+3sin(x) >1
Voici ma réponse : S=U(kϵZ)]k2π;2π3+k2π[S=U(kϵZ)]k2\pi ; \frac{2\pi}{3} + k2\pi[S=U(kϵZ)]k2π;32π+k2π[
-
@lala-o Bonjour,
Les objectifs principaux de ce site sont de fournir des pistes de résolution ou de vérifier les calculs indiqués.
As-tu transformé l'inégalité en faisant apparaître que la fonction sinus ou cosinus ?
-
BBlack-Jack dernière édition par
@lala-o a dit dans Inéquations trigonométrique :
Bonjour,
J'aimerais avoir une correction pour cet exercice : cos(x)+3sin(x)cos (x) + \sqrt3sin(x) cos(x)+3sin(x) >1
Voici ma réponse : S=U(kϵZ)]k2π;2π3+k2π[S=U(kϵZ)]k2\pi ; \frac{2\pi}{3} + k2\pi[S=U(kϵZ)]k2π;32π+k2π[Bonjour,
Ta réponse finale est correcte.Mais sans décrire les calculs qui t'y ont amené, on ne peut pas savoir si ceux-ci sont corrects.
Il arrive fréquemment que des erreurs se compensent en cours de développement et qu'on arrive à une solution finale exacte ... en ayant fait une ou des erreurs en cours de raisonnement.
-
Une piste : utilise les relations trigonométriques :
sin(a+b)=....sin(a+b) = ....sin(a+b)=....
cos(a−b)=....cos(a-b)= ....cos(a−b)=....Une vérification graphique :
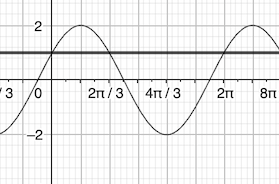
-
mtschoon dernière édition par mtschoon

Bonjour tout le monde,
@lala-o , comme indiqué, ta réponse finale est correcte.
On ignore comment tu as fait...ce qui est dommage, car on ne peut pas savoir si ta démarche est bonne.
Une piste possible simple :
En divisant par 222 :
12cosx+32sinx>12\dfrac{1}{2}cosx+\dfrac{\sqrt 3}{2}sinx\gt \dfrac{1}{2}21cosx+23sinx>21
c'est à dire,
cos(x−π3)>12cos(x-\dfrac{\pi}{3})\gt \dfrac{1}{2}cos(x−3π)>21