exercice probabilité

bonsoir j'ai un exercice que je n'arrive pas à comprendre comprendre.
Sur un dé cubique non pipé l’unedes faces est numérotée 1, n faces (0≤𝑛≤5)sont
numérotées 2 et les faces restantes sont numérotées 3. Les faces d’un second dé cubique non
pipé sont numérotées 1; 2; 3;4et 4. Les deux sont lancés simultanément.
Soit X la variable aléatoire qui à chaque lancer associe la somme des points marqués sur les
faces supérieures.

Démontre que: 𝑝(𝑋=6)=n+5/36
on suppose que n = 2.
a) Détermine la loi de probabilité de X.
b) Justifie que l’espérance Mathématique E(X) de X est égale à 5.
c) Calcule l’écart-type de X.
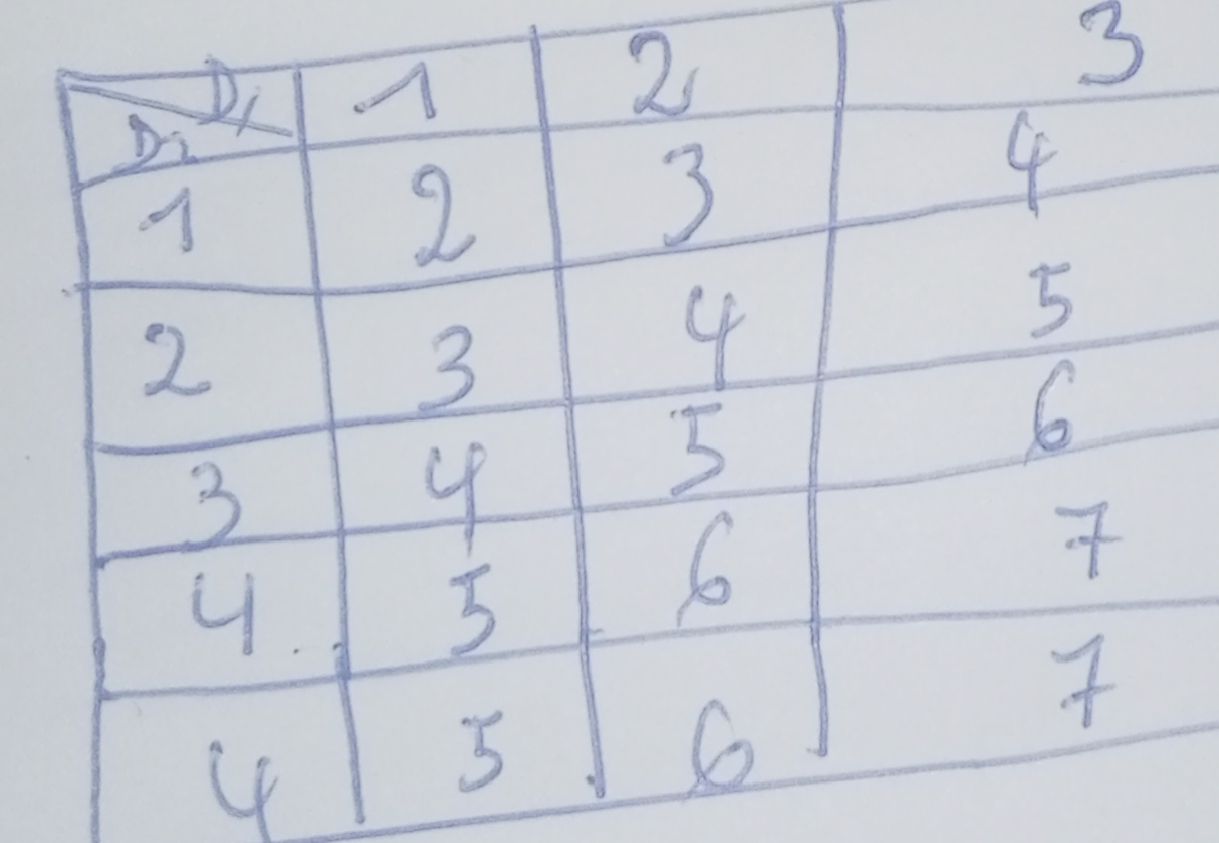
pour la première question j'ai réussi à faire un tableau mais je n'arrive pas à faire la démonstration

@jean-12 Bonsoir,

Pour la question 1,
Pour le premier dé ; 1 face 1, $n$ faces 2 (avec $n$ compris entre 0 et 5) et $5 - n$ faces 3.
Pour le second dé ; 1 face 1, 1 face 2, 1 face 3 et 2 faces 4 ? Il manque une face ?
Détermine le nombre de façons d'obtenir 6 :
Dé 1 : face 2 ; Dé 2 face 4 , donc $2 n$ possibilités
Dé 2 : .....

@Noemi bonsoir
Dé 2 face 3 et Dé 1 face 3 donc 5-n

@jean-12 a dit dans exercice probabilité :

Sur un dé cubique non pipé l’unedes faces est numérotée 1, n faces

J'ai retrouvé l'énoncé sur le net (seulement à 2 endroits) , voila une copie écran de la recherche :

Sans titre.png

Conclusion, le prof se contente de copier un énoncé quelque part et n'a même pas le courage de vérifier son exactitude.

@Black-Jack bonjour
moi j'avais constaté cela mais néanmoins, pouvez vous m'expliquez afin que je puisse comprendre

Sur ce lien: https://www.sunudaara.com/mathematiques/série-dexercices-probabilités-ts

Il y a un énoncé qui "ressemble" :

Le voici :

Sur un dé cubique, l'une des faces est numérotée 1, n faces sont numérotées 2 et les faces restantes sont numérotées 3.

Les faces d'un second dé cubique sont numérotées 1, 2, 2, 3, 4 et 4.

Les deux dés sont lancés simultanément et leurs faces ont la même probabilité de sortir en position supérieure.

Soit X

la variable aléatoire qui à chaque lancer associe la somme des points marqués sur les faces supérieures.

Déterminer n
pour que la probabilité de l'événement (X=6) soit égale à 7/36.
On choisit maintenant n=2.

Donner la loi de probabilité de X.
''''''''''
La suite de l'exercice est différente ...

Ici, les 6 faces du 2ème dé sont bien définies.
'''''''''''''''''''''''''''''''''''''''

Avec les données de cet énoncé corrigé:

Proba de faire 1 avec le dé 1 : P1(1) = 1/6
Proba de faire 2 avec le dé 1 : P1(2) = n/6
Proba de faire 3 avec le dé 1 : P1(3) = (5-n)/6

Proba de faire 1 avec le dé 2 : P2(1) = 1/6
Proba de faire 2 avec le dé 2 : P2(2) = 1/3
Proba de faire 3 avec le dé 2 : P2(3) = 1/6
Proba de faire 4 avec le dé 2 : P2(4) = 1/3

Pour faire 6 comme somme, on peut faire : (2 + 4) ou (3 + 3)
--> P(X=6) = (n/6) * (1/3) + (5-n)/6 * 1/6
P(X=6) = n/18 + (5-n)/36
P(X=6) = (2n + 5-n)/36
P(X=6) = (n+5)/36

Avec n = 2 :

a)

Proba de faire 1 avec le dé 1 : P1(1) = 1/6
Proba de faire 2 avec le dé 1 : P1(2) = 2/6 = 1/3
Proba de faire 3 avec le dé 1 : P1(3) = (5-2)/6 = 1/2

Proba de faire 1 avec le dé 2 : P2(1) = 1/6
Proba de faire 2 avec le dé 2 : P2(2) = 1/3
Proba de faire 3 avec le dé 2 : P2(3) = 1/6
Proba de faire 4 avec le dé 2 : P2(4) = 1/3

P(X=1) = 0 car ...
P(X=2) = 1/6 * 1/6 = 1/36
P(X=3) = 1/6 * 1/3 + 1/3 * 1/6 = 1/9
P(X=4) = ...

Continue.