Application affine et transformation d’un plan
-
MMMounah dernière édition par
Bonsoir
Le plan est rapporté au repère orthonorné ( 0 ; vec i ; vec J )
Partie A
- A tout point M du plan on associe le point M_{1} image de M par la symétrie orthogonale d'axe la droite d'équation y = x puis le point M' image de M_{1} par la symétrie orthogonale d'axe ( 0 ; vec i ).
a) Calculer les coordonnées x' y' de M' en fanction des coordonnées x et y de M.
b) Caractériser l'application qui transforme M en M'.
-
@Zeïnab-Mahamadou Bonjour,
Indique tes éléments de réponse et la question qui te pose problème.
-
mtschoon dernière édition par mtschoon

Bonjour,
@Zeïnab-Mahamadou , piste pour démarrer,
Schéma pour éclairer,
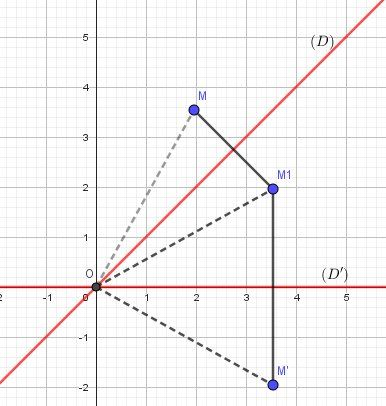
M(x,y)M(x,y)M(x,y)
M1(y,x)M_1(y,x)M1(y,x)
M′(y,−x)M'(y,-x)M′(y,−x)
Peut-être que ton cours te donne la nature du composé de 2 symétries axiales d'axes concourants sinon tu la trouves en raisonnant.
-
MMMounah dernière édition par
@Noemi bonsoir
C’est que j’arrive pas à démarrer si j’envoie lexo seulement
-
MMMounah dernière édition par
@mtschoon bonsoir
Je sais que la composée de deux symétries est une rotation
Laïus comme vous avez fait pour déterminer les coordonnées de M’ et M_1
-
BBlack-Jack dernière édition par
@Zeïnab-Mahamadou a dit dans Application affine et transformation d’un plan :
@mtschoon bonsoir
Je sais que la composée de deux symétries est une rotation
Laïus comme vous avez fait pour déterminer les coordonnées de M’ et M_1Bonjour,
Une rotation, OUI
Mais il faudrait préciser le centre, le rayon et l'angle de cette rotation.Piste:
Calculer |OM| et |OM'| ...
Et calculer OM→.OM′→\overrightarrow{OM} . \overrightarrow{OM'}OM.OM′
-
mtschoon dernière édition par mtschoon

Bonjour,
@Zeïnab-Mahamadou , si ton cours le prévoit, tu dois savoir précisemment de quelle rotation il s'agit.
Dans ce cas, tu l'appliques directement :
"Si les droites D et D' sont sécantes en un point O , la composée de la symétrie orthogonale par rapport à (D) suivie de la symétrie orthogonale par rapport ) (D') est la rotation de centre O et d'angle 2 ( D , D' )"Sinon, tu fais les calculs ; Black-Jack t'a donné une piste éventuelle.
Indique ta réponse sur cette rotation si tu souhaites une vérification.
-
mtschoon dernière édition par mtschoon

@Zeïnab-Mahamadou , tu indiques ne pas savoir déterminer les coordonnées de M1M_1M1 et M′M'M′
Je complète de schéma.
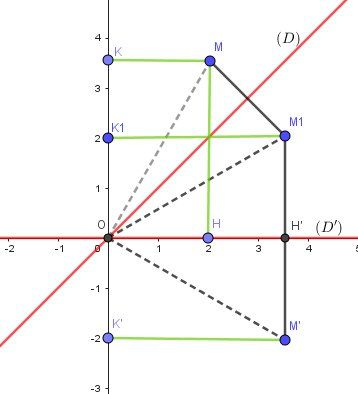
Coordonnées de M(x,y)M(x,y)M(x,y) :
OH‾=x\overline{OH}=xOH=x
OK‾=y\overline{OK}=yOK=yPar symétrie par rapport à (D) d'équation y=x (bissectrice de l'angle des deux axes de coordonnées), absisse et ordonnée sont échangées:
OK1‾=OH‾\overline{OK_1}=\overline{OH}OK1=OH
OH′‾=OK‾\overline{OH'}=\overline{OK}OH′=OKCoordonnées de M1(x1,y1)M_1(x_1,y_1)M1(x1,y1) :
OH′‾=x1=y\overline{OH'}=x_1=yOH′=x1=y
OK1‾=y1=x\overline{OK_1}=y_1=xOK1=y1=xPar symétrie par rapport à (D')droite portée par l'axe des abscisses) , M1M_1M1 et M′M'M′ ont mêmes abscisses et des ordonnées opposées.
Coordonnées de M′(x′,y′)M'(x',y')M′(x′,y′) :
OH′‾=x′=x1=y\overline{OH'}=x'=x_1=yOH′=x′=x1=y
OK′‾=y′=−y1=−x\overline{OK'}=y'=-y_1=-xOK′=y′=−y1=−xRegarde tout ça de près.
-
MMMounah dernière édition par MMounah
@mtschoon bonsoir
J’avais procédé par l’expression analytique, et j’ai trouvé le même résultat merci
-
MMMounah dernière édition par MMounah
@Black-Jack bonsoir
(OM)→(x;y)\overrightarrow{(OM)}(x;y)(OM)(x;y) et (OM’)→(y;−x)\overrightarrow{(OM’)}(y;-x)(OM’)(y;−x)
(OM)→.(OM’)→\overrightarrow{(OM)}.\overrightarrow{(OM’)}(OM).(OM’) = 0→\overrightarrow{0}0 non ?
Et l’angle n’as pas l’aire d’être nul
-
MMMounah dernière édition par
@Zeïnab-Mahamadou bonsoir
Voici le reste , aidez moi avec des pistes dans chaque question à partir de 2.
c) Au point M * [[x], [y]] on associe le point N de coordonnées X et Y telles que x = y + 1; y = - x + 1 (1)(c’est un système)
Montrer que cette transformation est une isométrie et la caractériser.-
Le point M décrivant la droite d'équation y = x déterminer l'ensemble décrit par N. quel est l'ensemble décrit par le milicu du segment [MN]?
-
Au point M [[x], [y]] on associe le point N' de coordonnées (x’;Y’x’;Y’x’;Y’) tel que X' = 3y + 1; Y = - 2x + 1 (2)
(Système aussi)
a) Quelle est la nature de l'ensemble E des points N' lorsque le point M décrit le cercle de centre O et de rayon 1.
b) Caractériser le transformé de E par la transformation (1).
-
-
mtschoon dernière édition par mtschoon

@Zeïnab-Mahamadou ,
Attention pour la fin de la partie A)
@Zeïnab-Mahamadou a dit dans Application affine et transformation d’un plan :
(OM)→(x;y)\overrightarrow{(OM)}(x;y)(OM)(x;y) et (OM’)→(y;−x)\overrightarrow{(OM’)}(y;-x)(OM’)(y;−x)
(OM)→.(OM’)→\overrightarrow{(OM)}.\overrightarrow{(OM’)}(OM).(OM’) = 0→\overrightarrow{0}0 non ?
Et l’angle n’as pas l’aire d’être nul@Zeïnab-Mahamadou , revois ton cours sur le produit scalaire.
Le produit scalaire de 2 vecteurs est un nombre , non un vecteur !OM→.OM′→=xy−yx=0\overrightarrow{OM}.\overrightarrow{OM'}=xy-yx=0OM.OM′=xy−yx=0
Donc vecteurs orthogonaux , donc angle droit.Evidemment , le produit scalaire ne te dit pas si l'angle droit est "direct" ou "indirect"
Pour avoir le sens de l'angle, analyse le graphique.
-
MMMounah dernière édition par
@mtschoon bonsoir
Merci j’ai compris , indiquer moi des pistes pour la prochaine question 2.
-
mtschoon dernière édition par

@Zeïnab-Mahamadou , bonjour,
Avant de regarder tes dernières demandes, merci d'indiquer avec précision la conclusion de la partie A.
Quelle rotation as-tu trouvée ?
-
mtschoon dernière édition par

Re-bonjour @Zeïnab-Mahamadou
Pour la rotation, j'espère que tu as trouvé OOO pour centre et −π2 [2π]-\dfrac{\pi}{2}\ [2\pi]−2π [2π] pour angle.
Je te démarre la question 222 si besoin.
Si j'ai bien compris (car ce que tu as écrit n'est pas clair...) , ce que tu cherches :M(x,y)M(x,y)M(x,y) avec y=xy=xy=x donc M(x,x)M(x,x)M(x,x).
N(X,Y)N(X,Y)N(X,Y) avec X=y+1X=y+1X=y+1 et Y=−x+1Y=-x+1Y=−x+1Si c'est bien ça :
X=x+1X=x+1X=x+1 et Y=−x+1Y=-x+1Y=−x+1Donc: x=X−1x=X-1x=X−1 et x=−Y+1x=-Y+1x=−Y+1
D'où : X−1=−Y+1X-1=-Y+1X−1=−Y+1 c'est à dire : X+Y−2=0X+Y-2=0X+Y−2=0
L'ensemble décrit par NNN est donc la droite d'équation X+Y−2=0X+Y-2=0X+Y−2=0Tu poursuis.
Bon travail.