Résolution d'équation de puissance

Bonjour,
j'ai besoin de la solution de cette équation
trouver x en fonction des constantes C1 et C2
[2*C1^(1/x)-1]^x=C2

merci d'avance

L'énoncé est complet ? Cette équation est donnée seule ?

@Noemi Je peut ajouter des informations supplémentaires tel que:
C1 et C2 sont positif est inferieur à 1
X est limité entre 1 et 4

Bonjour,

@Abdelhak-Benkaba , j'ai un gros doute sur ta question.

Si j'ai bien compris l'équation proposée (?), pour voir, j'ai fait travailler un solveur d'équation sur le net, en prenant un cas particulier $C1=C2=12C_1=C_2=\dfrac{1}{2}$ .

Aucun réponse trouvée pour $x$ , ni valeur exacte, ni valeur approchée....

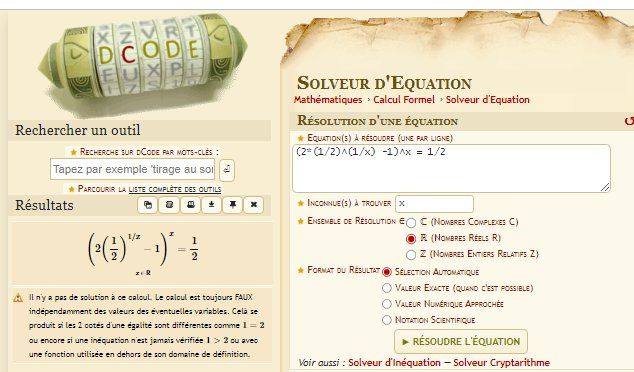
Bon courage , car cela dépend visiblement des valeurs prises pour $C_1$ et $C_2$ comprises entre $0$ et $1$ , pour que tu puisses avoir une solution réelle pour $x$ (comprise entre $1$ et $4$ ).
Une chose est sûre : tu ne peux pas trouver $x$ pour toutes les valeurs de $C_1$ et $C_2$ comprises entre $0$ et $1$

@Abdelhak-Benkaba , vérification graphique de l'exemple précédent :

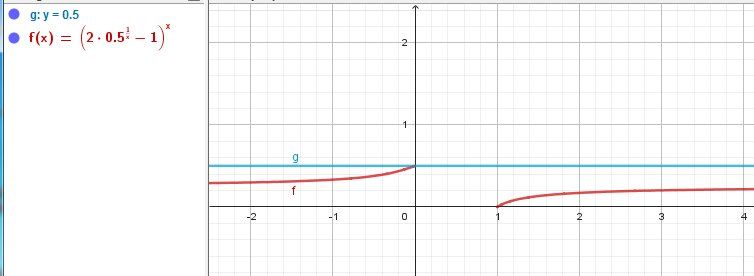
Pas de solution ( pour $x$ compris entre $1$ et $4$ ) avec les valeurs $C_1$ et $C_2$ égales à 0.5.

Bonjour,

On peut montrer qu'avec f(x) = [2.C1^(1/x) - 1]^x , f existe pour x > -ln(C1)/ln(2)

f est croissante sur [-ln(C1)/ln(2) ; 4]

Donc fmax = f(4) = [2.C1^(1/4) - 1]^4

Si C2 > [2.C1^(1/4) - 1]^4, il n'y a pas de solution réelle à [2.C1^(1/x) - 1]^x = C2

Si 0 < C2 < [2.C1^(1/4) - 1]^4, il y a une et seule solution à [2.C1^(1/x) - 1]^x = C2
Comme f est strictement croissante sur [-ln(C1)/ln(2) ; 4], on peut chercher par approximations successives, la valeur de x telle que [2.C1^(1/x) - 1]^x = C2

Par exemple avec C1 = 0,6 et C2 = 0,25
On calcule [2.C1^(1/4) - 1]^4 = [2*0.6^(1/4) - 1]^4 = 0,334...

Comme C2 < 0,334..., il y a une et une seule solution à [2*0,6^(1/x) - 1]^x = 0,25 que l'on cherche par approximations successives dans l'intervalle ]1 ; 4[
On trouve x = 1,25566...