Asymptote horizontale

[-lala-o]

Bonjour, je ne comprends pas comment calculer $li{m}_{x\to +\infty }{e}^{x.artcan(\frac{1}{x})}$.

[mtschoon]

@lala-o , bonjour,

Piste rapide,

Lorsque $x$ tens vers $+\infty$, $\frac{1}{x}$ tend vers $0$

$arctan(\frac{1}{x})\sim \frac{1}{x}$

$\underset{x\to +\infty }{\lim }$$e^{x\ast arctan(\frac{1}{x})}=e^1=e$

[-lala-o]

@mtschoon Bonjour, est-ce que $\infty \ast 0=0$ ou c'est un cas d'indétermination ?

[Noemi]

@lala-o Bonjour,

C'est un cas de limite indéterminée.

[mtschoon]

Bonjour,

@lala-o a dit dans Asymptote horizontale :

@mtschoon Bonjour, est-ce que $\infty \ast 0=0$ ou c'est un cas d'indétermination ?

Comme te dit @Noemi , oui, il y a indétermination s'il s'agit du produit d'une expression qui tend vers l'infini et l'autre qui tend vers 0.
Le produit ne tend pas forcément vers $0$ .

Par contre, si une des quantités est égale à 0 et pas seulement tendant vers $0$, alors là, le produit vaudra $0$

[-lala-o]

@mtschoon Je ne comprends pas la piste que vous m'avez donnée. Je pensais que arctan(0+)=0+ et donc +$\infty \ast 0^{+}$ est un cas d'indétermination. Pourquoi ici arctan(1/x) ne tend pas vers 0 mais est égal à 0?

[mtschoon]

@lala-o , j'explicite un peu.

Lorsqu'on a une indétermination, le but est de la lever.

Lorsque $x$ tend vers $+\infty$, $\frac{1}{x}$ tend vers 0 (par valeurs positives)
Donc, $arctan\frac{1}{x}$ tend vers $0$ (par valeurs positives)
$xarctan\frac{1}{x}$ prend donc la forme indéterminée "$0\times \infty$"

Il faut donc lever cette indétermination pour trouver la limite .

Pour cela, tu peux passer, par exemple, par les équivalents (comme il s'agit d'un produit, ça convient)

Tu dois savoir que pour X voisin de $0$ , $arctan(X)\sim X$

Donc, tu poses $X=\frac{1}{x}$

Lorsque x tend vers $+\infty$, $\frac{1}{x}$ tend vers $0$
$arctan(\frac{1}{x})\sim \frac{1}{x}$
$xarctan(\frac{1}{x})\sim x\times \frac{1}{x}$
$xarctan(\frac{1}{x})\sim 1$
$e^{xarctan(\frac{1}{x})}\sim e^1$

Deux fonctions équivalentes ont même limite
donc :
$\underset{x\to +\infty }{\lim }{e}^{xarctan(\frac{1}{x})}=e^1=e$

[mtschoon]

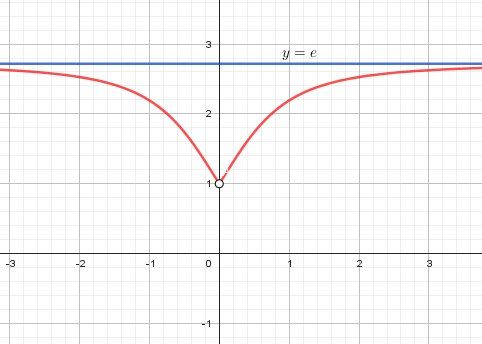
@lala-o , Illustration graphique
La droite d'équation $y=e$ est asymptote horizontale à la courbe.