Minimant, maximant local

[-lala-o]

Bonjour, voici l'énoncé :
$f(x)=e^{xarctan\frac{1}{x}}$ si $xϵR_0$
$f(x)=2$ si $x=0$
Le point x=0 est-il un minimant ou un maximant local de f?

D'abord, je ne voit pas très bien la différence entre le maximant/minimant et le maximum/minimum. Est-ce la même chose?

Si le but est de trouver les extremum, je ne comprends pas très bien comment faire dans ce cas-ci.

[Noemi]

@lala-o Bonjour,

Vérifie l'énoncé.
Etudie les variations de la fonctions.

[mtschoon]

Bonjour,
Minimant, maximant ? ? ? je n'ai jamais entendu parler de ces termes ( et mon dictionnaire français ne le connait pas non plus...)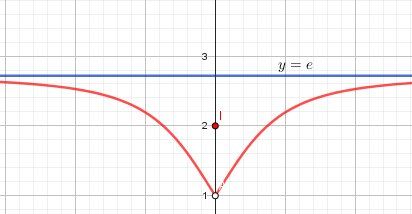

@lala-o , tu avais donné cette fonction ( sans f(0) ) dans un topic relatif à l'asymptote horizontale ($y=e$)

Pour t'éclairer, je te remets le schéma en le complétant avec le point $I(0.2)$
La représentation graphique est donc en rouge ( courbe et point I)

x=0 correspond ainsi à un maximum local.

Pour le prouver, le plus rapide est de chercher la limite de $f(x)$ lorsque $x$ tend vers $0$ ( par valeurs positives et par valeurs négatives )
Tu trouves que cette limite vaut $1$

Vu que $f(0)=2$ (point I), $0$ est un maximum local.