suite Un+1 par apport a n et Un

nous avons une suite
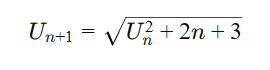
U(n+1)=sqrt(((Un)^2)+2n+3)
et U0=1
prouver qu'elle est arithmétique

@omar-ackerman Bonsoir, (Marque de politesse à ne pas oublier.

Une piste :
Exprime la différence : $U_n^2-U_0^2= ...$
En partant de : $U_1^2-U_0^2= ...$
$U_2^2-U_1^2= ...$
.....

Bonjour,

Calcule numériquement les quelques premiers termes de la suite ...

U0 = 1
U1 = ... = 2
U2 = ...
U3 = ...

En examinant ces résultats, tu fais une conjecture (supposition) de ce que pourrait être Un ...
Tu devrais pouvoir "conjecturer" que Un = n + 1

Il reste à démonter que cette conjecture est correcte ... en la démontrant par récurrence par exemple.

Bonjour,

@omar-ackerman , un petit plus si besoin,

Après avoir conjecturé que $U_n=n+1$ , la récurrence se fait très bien.

Hypothèse à un ordre n de $N$ : $U_n=n+1$

Conclusion à prouver $U_{n+1}=n+2$

Piste pour la preuve :

$Un+1=(n+1)2+2n+3U_{n+1}=\sqrt{(n+1)^2+2n+3}$

Après développement/simplification:
$Un+1=n2+4n+4U_{n+1}=\sqrt{n^2+4n+4}$

On reconnait une identité remarquable sous le radical, qui après simplification, permet de déduire : $U_{n+1}=n+2$ ,

Bon calcul.