étude de fonction problème
-
Gguillaume M dernière édition par
Bonjour pouvez vous m'aider à comprendre pourquoi il n'y a pas d'AH et peut-être vite me rappeler quand est-ce que le 0 est négatif ou positif pour savoir le signe de l'infini dans ce cas-ci Merci:
Etudier avec précision la fonction suivante:
f(x)=ln((x-4)/2x)+x
-
AAnas dernière édition par
J'ai pas vraiment saisi ta question
-
@guillaume-M Bonjour,
Commence par déterminer le domaine de définition de cette fonction.
-
mtschoon dernière édition par mtschoon

Bonjour,
@guillaume-M a dit dans étude de fonction problème :
Bonjour pouvez vous m'aider à comprendre pourquoi il n'y a pas d'AH et peut-être vite me rappeler quand est-ce que le 0 est négatif ou positif pour savoir le signe de l'infini dans ce cas-ci Merci:
Etudier avec précision la fonction suivante:
f(x)=ln((x-4)/2x)+x@guillaume-M , tes questions ne sont vraiment pas claires...
1 ) Quand tu dis "AH", tu parles d'asymptote horizontale ?
Pour que la représentation graphique de fff ait une asymptote horizontale d'équation y=ay=ay=a (a constante réelle), il faudrait que la limite de f(x)f(x)f(x) lorsque x tend vers +∞+\infty+∞ ou −∞-\infty−∞ soit aaa
Ce n'est pas le cas de la fonction fff que tu donnes ici.2 ) le nombre réel 000 est à la fois positif et négatif
0∈R0\in R0∈R,
0∈R+0\in R^+0∈R+
0∈R−0\in R^-0∈R−
Tu as dû mal formuler ta question...3 ) Etude de f(x)=ln(x−42x)+xf(x)=ln\biggr(\dfrac{x-4}{2x}\biggr)+xf(x)=ln(2xx−4)+x
Comme te l'a indiqué @Noemi , la première chose à faire est de déterminer l'ensemble de défintion.
Condition d'existence (due au ln)
x−42x>0\dfrac{x-4}{2x}\gt 02xx−4>0
Tu peux faire un tableau de signes et tu trouves :
Df=]−∞,0[∪]4,+∞[D_f=]-\infty , 0[\cup ]4 ,+\infty[Df=]−∞,0[∪]4,+∞[Sur DfD_fDf, fff est dérivable et tu dois trouver, sauf erreur :
f′(x)=4x(x−4)+1f'(x)=\dfrac{4}{x(x-4)}+1f′(x)=x(x−4)4+1
f′(x)>0f'(x)\gt 0f′(x)>0
fff est strictement croissante sur ]−∞,0[]-\infty , 0[]−∞,0[ et sur ]4,+∞[]4 ,+\infty[]4,+∞[Tu fais le tableau de variation de fff.
Si c'est demandé dans ton exercice, tu cherches les limites aux bornes du domaine de définition et éventuellement les asymptotes à la représentation graphique.
Reposte si tu as besoin de compléments en étant précis dans ta question.
-
mtschoon dernière édition par

Tableau de variation
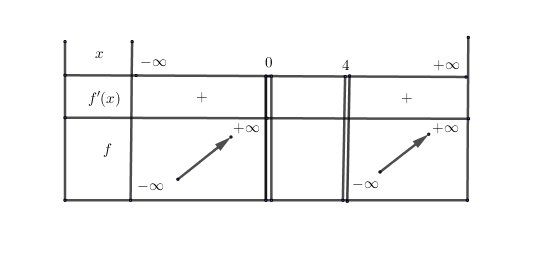
-
Gguillaume M dernière édition par
@mtschoon Merci beaucoup vous m'avez éclairez et encore désolé pour ma formulation maladroite

-
mtschoon dernière édition par

De rien @guillaume-M.
C'est très bien si les explications données ont été suffisantes.