Intégration 3D - sphère
-
-lala-o dernière édition par

Bonjour,
J'aimerais avoir une correction pour cet exercice : "calculer le volume d'eau d'une sphère remplie jusqu'à une certaine hauteur h"
Voici ma résolution :
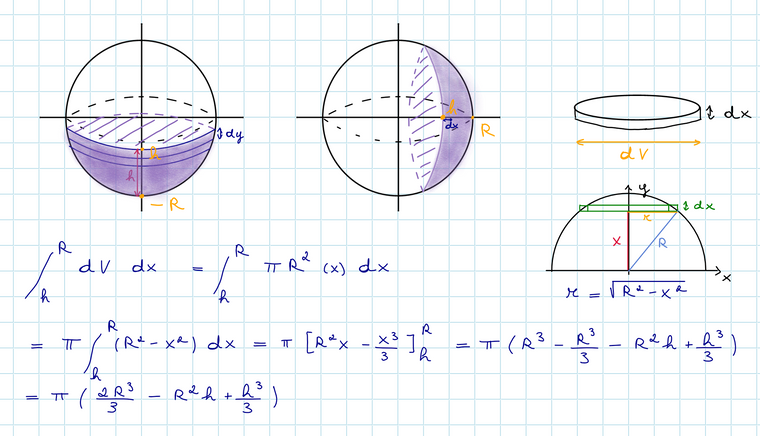
-
@lala-o Bonjour,
La démarche est correcte.
Les bornes de l'intégrale sont à revoir. Au départ c'est −R-R−R.
-
BBlack-Jack dernière édition par
Bonjour,
Dessin de gauche :
V=π∫−RR+hx2 dyV = \pi \int_{-R}^{R+h} x^2\ dyV=π∫−RR+hx2 dy
V=π∫−RR+h(R2−y2) dyV = \pi \int_{-R}^{R+h} (R^2-y^2)\ dyV=π∫−RR+h(R2−y2) dy
V=π[R2y−y33]−R−R+hV = \pi [R^2y - \frac{y^3}{3}]_{-R}^{-R+h} V=π[R2y−3y3]−R−R+h
V=π.(R2(h−R)−(h−R)33+R3−R33)V = \pi .(R^2(h-R) - \frac{(h-R)^3}{3} + R^3 - \frac{R^3}{3})V=π.(R2(h−R)−3(h−R)3+R3−3R3)
V=π(R2h−R3−h3−R3+3hR2−3h2R3+R3−R33)V = \pi (R^2h -R^3 - \frac{h^3-R^3+3hR^2-3h^2R}{3}+R^3-\frac{R^3}{3})V=π(R2h−R3−3h3−R3+3hR2−3h2R+R3−3R3)
V=π.h2.(R−h3)V = \pi.h^2.(R-\frac{h}{3})V=π.h2.(R−3h)
V=π.h23.(3R−h)V = \frac{\pi.h^2}{3}.(3R-h)V=3π.h2.(3R−h)Sans relecture.