Calcul de probabilité conditionnelle

[tedactez poli]

Bonjour à tous,

J'ai rencontré un exercice intéressant en mathématiques que je voudrais partager avec vous pour obtenir de l'aide.

Dans une école d'ingénieurs, on s'intéresse à 100 élèves.
Parmi ces 100 élèves, 60 ont déjà voyagé en avion, 40 par bateau, et 25 ont utilisé les deux moyens de transport.
On cherche la probabilité que 2 élèves choisis au hasard aient voyagé par bateau sachant qu'ils n'ont jamais pris l'avion.

[mtschoon]

@tedactez-poli (TanTanBPM) , bonjour,

Piste pour démarrer,

Je te conseille de faire un diagramme pour clarifier les dénombrements utiles.
Je t'en joins un.

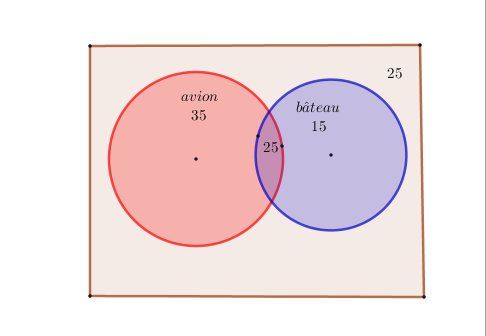
25 élèves ont utilisé avion et bateau

60-25=35
35 élèves ont utilisé avion seul

40-25=15
15 élèves ont utilisé bateau seul

25+35+15=75
100-75=25
25 élèves ont utilisé ni avion, ni bateau

Pour ta question (pense aux combinaisons) :

Evènement A : deux élèves choisis au hasard ont voyagé par bateau
Evènement B : deux élèves choisis au hasard n'ont jamais pris l'avion.

Tu cherches dont $p_B(A)$

Tu sais que : $p_B(A)=\frac{p(A\cap B)}{p(B)}$

Ici, c'est plus simple de passer directement par les cardinaux :
$p_B(A)=\frac{card(A\cap B)}{card(B)}$

Indique les résultats de tes calculs si tu le souhaites.

[mtschoon]

@tedactez-poli ,

Je t'indique ce que tu dois trouver

Sauf erreur, tu dois trouver $\frac{105}{780}=\frac{7}{52}$

Bons calculs.