Cercle géométrie/ Équation d'un cercle tangent aux axes de coordonnées

Bonsoir,s'il vous plaît j'aimerais obtenir de l'aide pour trouver l'équation d'un cercle tangent aux axes de coordonnées aux points (2,0) et (0,-2) et dont le centre se trouve sur la deuxième bissectrice aux axes.
En travaillant géométriquement j'ai pû trouver l'équation mais je n'arrive pas à trouver analytiquement.
Merci d'avance

@linjos Bonsoir,

Si O est le centre du cercle : $OM^2= R^2$

@Noemi O n'est pas le centre du cercle. En fait, il faut trouver le centre pour pouvoir trouver l'équation du cercle

Bonsoir @linjos,
Pour trouver le centre du cercle (qui de ce que j'imagine est en (2,-2)), tu peux utiliser le fait que les tangentes sont perpendiculaires aux rayons, non?

Bonjour,

Illustration graphique
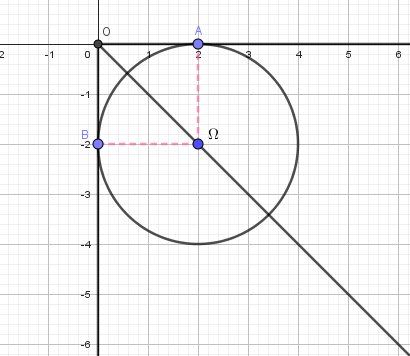
cercle tangent.jpg
Equation $x-2)^2+(y+2)^2=4$

@linjos , je vois que tu as posté en 5ème / 6ème .
Tu as dû te tromper de rubrique (ou tu n'utilises pas les programmes français).
La modération le déplacera peut-être.

@linjos

J'ai noté $O$ le centre du cercle et donné la relation.
Si tu appelle $Ω\Omega$ le centre du cercle alors : : $ΩM2=R2\Omega M^2= R^2$

Bonjour,

Merci à la modération d'avoir déplacé ce topic.

@jacques_atique j'y aie pensé mais je vois pas comment faire.

@Noemi mais le rayon n'est pas donné dans l'exercice.

@mtschoon désolé,je serai plus attentif prochainement

@linjos

le rayon : $R = 2$ .

@linjos , bonsoir,

Tu as eu tout ce qu'il faut mais tu sembles ne pas bien comprendre.
Relis toutes les réponses.

J'essaie de résumer :
$A (2, 0)$ . La tangente en $A$ au cercle cherché est la droite $(O A)$ (droite portant axe des abscisses)
La perpendiculaire en $A$ à $(O A)$ est la droite d'équation $x=2\boxed{x=2}$
$B (0, - 2)$ . La tangente en $B$ au cercle cherché est la droite $(O B)$ (droite portant axe des ordonnées)
La perpendiculaire en $B$ à $(O B)$ est la droite d'équation $y=−2\boxed{y=-2}$

Le centre $Ω\Omega$ du cercle cherché est le point d'intersection de ces deux droites d'équations respectives $x = 2$ et $y = - 2$
$Ω\Omega$ a donc pour coordonnées $(2,−2)\boxed{(2,-2)}$

Le cercle cherché, de centre $Ω\Omega$ passe par $A$ et $B$
Le rayon est donc :
$R=ΩA=ΩB=2\boxed{R= \Omega A=\Omega B=2}$

Connaissant le centre et le rayon, tu donnes l'équation du cercle de la façon que tu as vu dans ton cours.

Bonne reflexion.

@mtschoon merci beaucoup
Désolé d'avoir donner cette impression.
J'ai pu trouver la réponse à 18h du jour précédent.
Du moins j'ai eu à commencer la saisie à 18 h

@linjos , si tu as compris, c'est très bien (et c'est encore mieux si tu as trouvé tout seul !)
Bon travail .