Exercice de Suiteeees
-
tra va dernière édition par tra va
Bonjour, dans un exercice je trouve : soit n appartient à l'ensemble N , on considère dans cette question à l'équation en inconnu x F(x) = n montrer que l'équation E(n) admet une unique solution notée (U)0. Avant on a la fonction f définie sur r alors que F de X = exponentielle x - exponentielle - X on étudie F prime on a construit le tableau de variation et on a dessiné la courbe CF représentative et la tangente.
-
mtschoon dernière édition par mtschoon

@tra-va , bonjour,
Ton énoncé est dur à lire...
J'espère avoir à peu près compris...f(x)=ex−e−xf(x)=e^x-e^{-x}f(x)=ex−e−x
f′x)=ex+e−xf'x)=e^x+e^{-x}f′x)=ex+e−x
f′(x)>0f'(x) \gt 0f′(x)>0
Tableau de variation
(j'ai ajouté (0,0) en vu de la question relative à la suite).
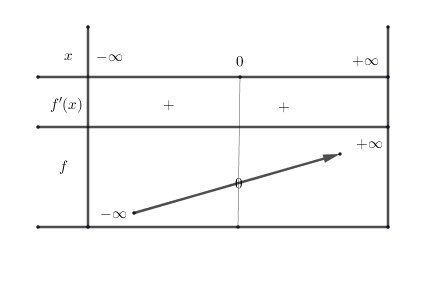
En restreignant l'étude à [0,+∞[[0,+\infty[[0,+∞[ , fff est définie dérivable donc continue et strictement croissante de [0,+∞[[0,+\infty[[0,+∞[ vers [0,+∞[[0,+\infty[[0,+∞[
fff est donc une bijection de [0,+∞[[0,+\infty[[0,+∞[ vers [0,+∞[[0,+\infty[[0,+∞[Donc, tout élément yyy de [0,+∞[[0,+\infty[[0,+∞[ (ensemble d'arrivée) a un antécédent unique xxx dans [0,+∞[[0,+\infty[[0,+∞[ (ensemble de départ).
(Tu peux parler de bijection réciproque si tu connais)En particulier, tout naturel nnn de l'ensemble d'arrivée a un antécédent unique UnU_nUn de l'ensemble de départ, c'est à dire tel que f(Un)=nf(U_n)=nf(Un)=n
On peut ainsi définir une suite (Un)(U_n)(Un) de termes positifs antécédents des valeurs nnn naturels de l'ensemble d'arrivée.
Le premier terme de cette suite pour n=0n=0n=0 est U0=0U_0=0U0=0
-
mtschoon dernière édition par mtschoon

@tra-va ,
Illustration graphique
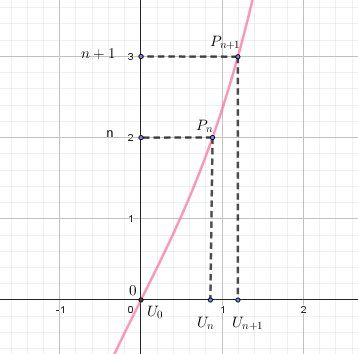
Pour tout nnn de NNN, Un+1>UnU_{n+1}\gt U_nUn+1>Un
Cette suite (Un)(U_n)(Un), de premier terme U0=0U_0=0U0=0 , à termes positifs, est strictement croissante et tend vers +∞+\infty+∞ lorsque nnn tend vers +∞+\infty+∞