Probabilité, espérance

Bonsoir
Soit y une variable aléatoire vérifiant les conditions suivantes.
•Y prend les Valeurs 1; -1; 2 avec les probabilités respectives $e^a, e^b ,e^c$ ; ou a, b, c sont dans cet ordre trois termes consécutifs d'une suite arithmétique de raison r.
L'espérance mathématique de Y est égale à 1.
1.montre que : système : $e^b(e^{-r}+1+e^r=1$
$e^b(e^{-r}-1+2e^r=1$
2.calculer a,b,c
3.Montrobs que l’écart type de Y est égale à $2217\dfrac{2\sqrt{21}}{7}$
Aider moi

@MMounah , bonsoir,

Piste pour démarrer (je n'ai pas fait les calculs)

$a = b - r$ et $c = b + r$

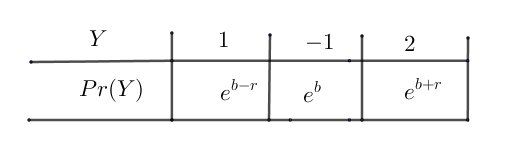
La somme des probabilité vaut , ce qui te donne l'égalité :
$e^{b-r}+e^b+e^{b+r}=1$
En mettant $e^b$ en facteur, tu obtiens :
$eb(e−r+1+er)=1\boxed{e^b(e^{-r}+1+e^{r})=1}$

Par définition de la moyenne, tu obtiens :
$1(e^{b-r})+(-1)e^b+2(e^{b+r})=1$
En mettant $e^b$ en facteur, tu obtiens :
$eb(e−r−1+2er)=1\boxed{e^b(e^{-r}-1+2e^r)=1}$

Tu résous le système pour trouver $b$ et $r$ ( et tu déduis ensuite $a$ et $c$ )

Bons calculs.

@mtschoon bonjour
$e−r+1+er=1ebe^{-r}+1+e^r=\dfrac{1}{e^b}$
$e−r−1+2er=1ebe^{-r}-1+2e^r=\dfrac{1}{e^b}$

L’addition donne
$2+3erer\dfrac{2+3e^r}{e^r}$ $=2eb=\dfrac{2}{e^b}$
Je fait le produit en X??

@MMounah Bonjour,

Soustrais les deux équations.

Bonjour,

Come te le dit @Noemi , en retranchant membre à membre, tu dois obtenir;
$e^b(2-e^r)=0$

Tua as un produit de facteurs nuls, donc tu peux terminer .

@mtschoon bonsoir
b=0 et r= ln(2) ??

@MMounah

Oui pour $r = l n 2$ mais non pour $b$
$e^b=0$ est impossible vu que $eb>0e^b\gt 0$

Remplace $r$ par $l n 2$ dans une équation de départ pour avoir $b$

@mtschoon
b=7/2
Donc a=7/2-ln(2) et c=7/2+ln(2)

@mtschoon
Bonjour
Pour l’écart type
Je calcule $(e72−ln2+e72+4e72+ln2)−1(e^{\frac{7}{2}-ln2}+e^{\frac{7}{2}}+4e^{\frac{7}{2}+ln2})-1$
Je pourrais mettre en facteurs mais c’est le 4 qui me bloque

@MMounah

Vérifie le calcul pour $b$ , sauf erreur, tu dois trouver : $ln(\dfrac{2}{7})$

Bonjour,

@MMounah a dit dans Probabilité, espérance :

@mtschoon
b=7/2
Donc a=7/2-ln(2) et c=7/2+ln(2)

L'expression que tu as trouvée pour $b$ n'est pas bonne

Je trouve la même valeur que @Noemi pour $b$ :
$b=ln(27)\boxed{b=ln\biggr(\dfrac{2}{7}\biggr)}$

@MMounah
Utilise une des expressions de l'énoncé qui ont été démontrées avec $e^b$ en facteur

$r = l n 2$ <=> $e^r=2$

Par exemple, avec la première équation trouvée :

$e^b(e^{-ln2}+1+e^{ln2})=1$
$eb(1eln2+1+eln2)=1e^b(\dfrac{1}{e^{ln2}}+1+e^{ln2})=1$
Tu remplaces $e^{ln2}$ par $2$ et tu continues pour trouver $e^b$ puis $b$

@mtschoon oui j’ai trouvé merci et l’écart type ?

Pour l'écart -type $σ\sigma$ , applique la définition de ton cours

$σ=ea(1−E(Y))2+eb(−1−E(Y))2+ec(2−E(Y))2\sigma=\sqrt{e^a(1-E(Y))^2+e^b(-1-E(Y))^2+e^c(2-E(Y))^2}$

@mtschoon bonsoir
Ça peut marcher avec $V(y)\sqrt{V(y)}$ Avec $V(y)=yi^2P(Y=yi)-(E(yi))^2$ ```
code_text

@MMounah , bonjour,
Un lien pour les définitions
https://www.bibmath.net/dico/index.php?action=affiche&quoi=./v/variance.html

@mtschoon mercii je trouve $sqrt127sqrt{\frac{12}{7}}$

@MMounah ,

La valeur que tu trouves pour l'écart type est bonne.

Il te reste à la transformer ( en multipliant numérateur et dénominateur par $7\sqrt 7$ puis en décomposant un peu le numérateur ) pour obtenir l'expression demandée.

@mtschoon $(7)(12)=(84)(\sqrt{7})(\sqrt{12})=(\sqrt{84})$ =2\sqrt{21}

@MMounah , bonsoir,

OUI,
$127=12×77=847=2217\sqrt{\dfrac{12}{7}}=\dfrac{\sqrt{12\times 7}}{7}=\dfrac{\sqrt{84}}{7}=\dfrac{2\sqrt{21}}{7}$

Je pense que maintenant tout ton exercice est bon.

@mtschoon ouii madame merci beaucoup

De rien @MMounah et bon travail.