exercice de probabilité conditionnelle

[tra va]

Bonjour à tous .Dans un exercice de proba conditionnelle. Soient
A, B et 𝐶 trois événements. On suppose que P(A)=P(B)=0,2
P(C)=0,8
P(A inter B barre)=0,1 et que B inter C = ensemble vide
1/ P(B) sachant A , P(A) sachant B et P(B) sachant C
Peut on calculer P (A inter C).

[Black-Jack]

Bonjour,

Proposition non vérifiée et donc méfiance.

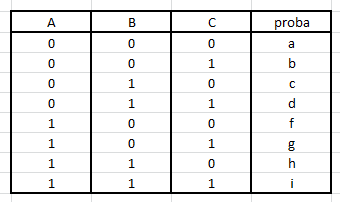
En traduisant les propoitions, on a le système :

f+g+h+i = 0,2
c+d+h+i = 0,2
b+d+g+i = 0,8
f+g = 0,1
d+i = 0

6 équations à 8 inconnues, on ne peut donc pas tout calculer, mais on peut quand même avancer ...

h+i = 0,1
c+h = 0,2
b+g = 0,8
f+g = 0,1
d+i = 0

d = 0
i = 0
h = 0,1
c = 0,1
b+g = 0,8
f+g = 0,1

P(B) sachant A = (h+i)/(f+g+h+i) = (0 + 0,1)/(0,1 + 0,1 + 0) = 1/2
P(A) sachant B = (h+i)/(c+d+h+i) = (0,1 + 0)/(0,1 + 0 + 0,1 + 0) = 1/2
P(B) sachant C = (d+i)/(b+d+g+i) = (0 + 0)/(b + 0 + 0,8 - b + 0) = 0/0,8 = 0

P(A inter C) = g + i = g = 0,8 - b
Mais b n'est pas connu et donc P(A inter C) n'est pas calculable.

---

A vérifier, bien entendu.