volume de primitives et intégrales
-
Mmanon.kpn dernière édition par
Je ne comprends pas mon erreur sachant que la réponse est 28000/3 pi cm3 !
Exercice 11Un pot de fleurs a la forme d’un tronc de cône.
Ses deux disques de base ont respectivement 10 cm et 20 cm de rayon. Sa hauteur est de 40 cm.
De combien de cm³ de terreau doit-on disposer afin de remplir ce pot pour y faire des semis ? On considère que le pot sera rempli à ras-bord et on ne tiendra pas compte de l’épaisseur du pot.
Représente le tronc de cône dans un repère adéquat afin de pouvoir aisément calculer son volume.
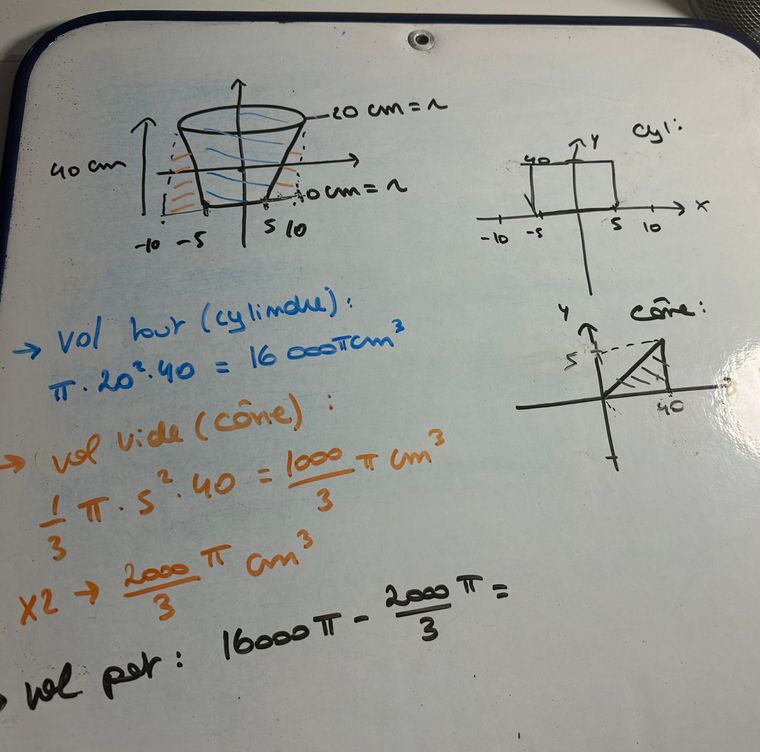
-
BBlack-Jack dernière édition par
Bonjour,
Ton calcul de volume est fantaisiste.
Ton calcul pour le "vide" est faux, il n'est pas du tout équivalent à celui d'un cône.Pour un tronc de cône, on a :
V=π.h3.(R2+r2+Rr)V = \frac{\pi.h}{3}.( R^2+r^2+Rr)V=3π.h.(R2+r2+Rr)
-
BBlack-Jack dernière édition par
Rebonjour,
Démo de la formule que j'ai donnée dans mon post précédent :
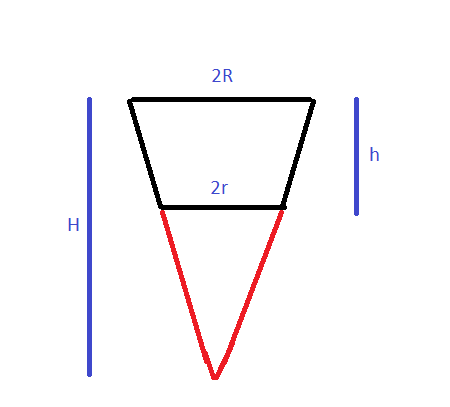
H/R = (H-h)/r
--> H = hR/(R-r)V = 1/3.Pi.R².H - (1/3).Pi.r².(H-h)
V = 1/3.Pi.H(R²-r²) + 1/3.Pi.r².h
V = 1/3.Pi.hR.(R²-r²)/(R-r) + 1/3.Pi.r².h
V = 1/3.Pi.hR.(R-r)(R+r)/(R-r) + 1/3.Pi.r².h
V = 1/3.Pi.hR.(R+r) + 1/3.Pi.r².h
V = 1/3.Pi.h.(R² + Rr + r²)