Alignement de points
-
CChris21300 dernière édition par
Bonjour à tous,
je suis bloqué sur le problème suivant :
ENONCE
ABCDEFGH est un cube. I milieu de [HF].
M vérifie : 2IM→=MA→2\overrightarrow{IM}=\overrightarrow{MA}2IM=MA- Exprimez AM→\overrightarrow{AM}AM en fonction deAI→\overrightarrow{AI}AI
- Démontrez que E,M et C sont alignés (sans utiliser de repère
- même question avec repère
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−---------------------------------−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Pour les questions 1 et 3 je n'ai pas de problème.
Par contre je ne parviens pas à faire la 2).
Il faut montrer que EM→=kEC→\overrightarrow{EM}=k\overrightarrow{EC}EM=kEC et me semble-t-il décomposer EM→\overrightarrow{EM}EM afin de faire apparaitre du EC→\overrightarrow{EC}EC
mais je n'y parviens pas ..Pourriez-vous me donner le début du chemin svp ?

Merci par avance

Je vous joins une petite capture de ma construction geogebra pour rendre la chose plus lisible

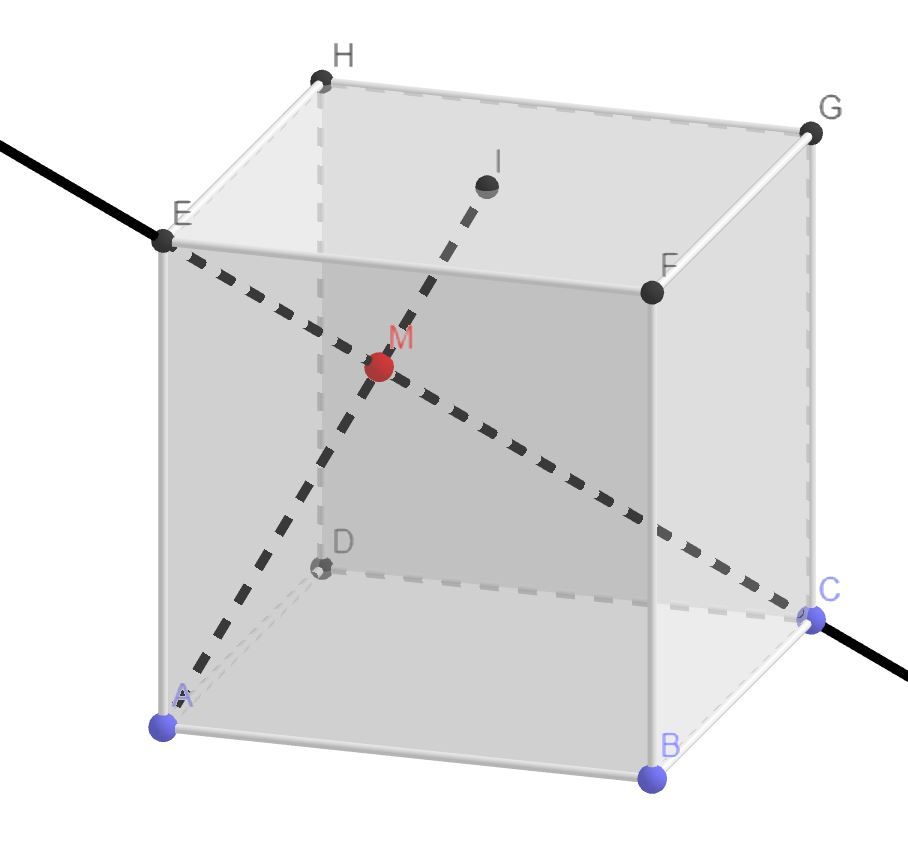
-
BBlack-Jack dernière édition par
Bonjour,
Les diagonales de EHGF (carré) se coupent en leur milieu ---> I est le milieu de [EG] (1)
EM→=EI→+IM→\overrightarrow{EM} = \overrightarrow{EI} + \overrightarrow{IM}EM=EI+IM
avec (1) --> EM→=12EG→+12MA→\overrightarrow{EM} = \frac{1}{2} \overrightarrow{EG} + \frac{1}{2} \overrightarrow{MA}EM=21EG+21MA
(et EG→=AC→(car...)\overrightarrow{EG} = \overrightarrow{AC} (car ...)EG=AC(car...) --->
EM→=12AC→+12MA→\overrightarrow{EM} = \frac{1}{2} \overrightarrow{AC} + \frac{1}{2} \overrightarrow{MA}EM=21AC+21MA
EM→=12(AC→+MA→)\overrightarrow{EM} = \frac{1}{2} (\overrightarrow{AC} + \overrightarrow{MA})EM=21(AC+MA)
EM→=12MC→\overrightarrow{EM} = \frac{1}{2} \overrightarrow{MC}EM=21MCEt donc les points E, M et C sont alignés.
-
CChris21300 dernière édition par
Arf .... comme tout est simple ainsi exprimé !
Merci beaucoup @Black-Jack ...J'avais oublié d'utiliser les propriétés du cube grrrMerci encore
