Problème d'optimisation construire un réservoir en zinc

[sonic5791]

Bonjour

Je bloque sur le problème d'optimisation (dérivée) ci-dessous. J'ai l'impression qu'il me manque une donnée .

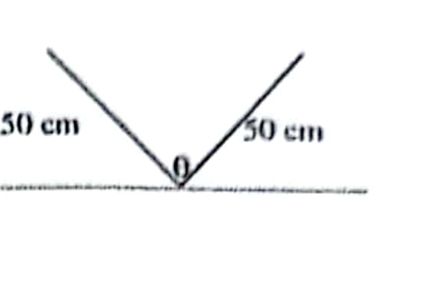
Voici l'énoncé : on construit un réservoir en pliant une feuille de zinc de 1 m de large en 2 et en fermant les 2 extrémités.
Quelle doit être la valeur de l'angle teta pour que la capacité du réservoir soit maximale. (

Merci pour votre aide ou indice

[Noemi]

@sonic5791 Bonjour,

Exprime le volume en fonction de l'angle $\theta$.

[JackAtik]

Bonjour, @sonic5791

Je ne suis pas trop sûr de moi donc j'attendrai un avis plus expert...

Pour moi la largeur de la feuille de zinc ne variant pas, on peut se borner à trouver l'aire maximale du triangle en fonction de $\theta$.

Si on nomme h la hauteur du triangle et c le demi côté horizontal, on a $h=50\cdot cos\frac{\theta }{2}$ et $l=50\cdot sin\frac{\theta }{2}$

D'où la surface S :
$S=50^2\times cos\frac{\theta }{2}\cdot sin\frac{\theta }{2}$

Puis en se servant de la formule :
$cos(a)\times sin(a)=\frac{1}{2}\times sin(2a)$

On déduit $S=50^2\times \frac{1}{2}\cdot sin\theta$

Et la surface serait donc maximale pour $\theta =\frac{\pi }{2}$

[Noemi]

@jacques_atique

C'est correct.

[JackAtik]

@Noemi merci de la confirmation.