Possibilité de faire un exercice

Bonjour.
Je suis au CNED, et j'ai un contrôle à envoyer, mais j'aimerais savoir si l'exercice est faisable.
Je ne souhaite absolument pas la réponse; juste savoir s'il est possible de le faire; car j'ai beau effectuer des calculs dans tous les sens; il y a des incohérences
Merci d'avance pour vos réponses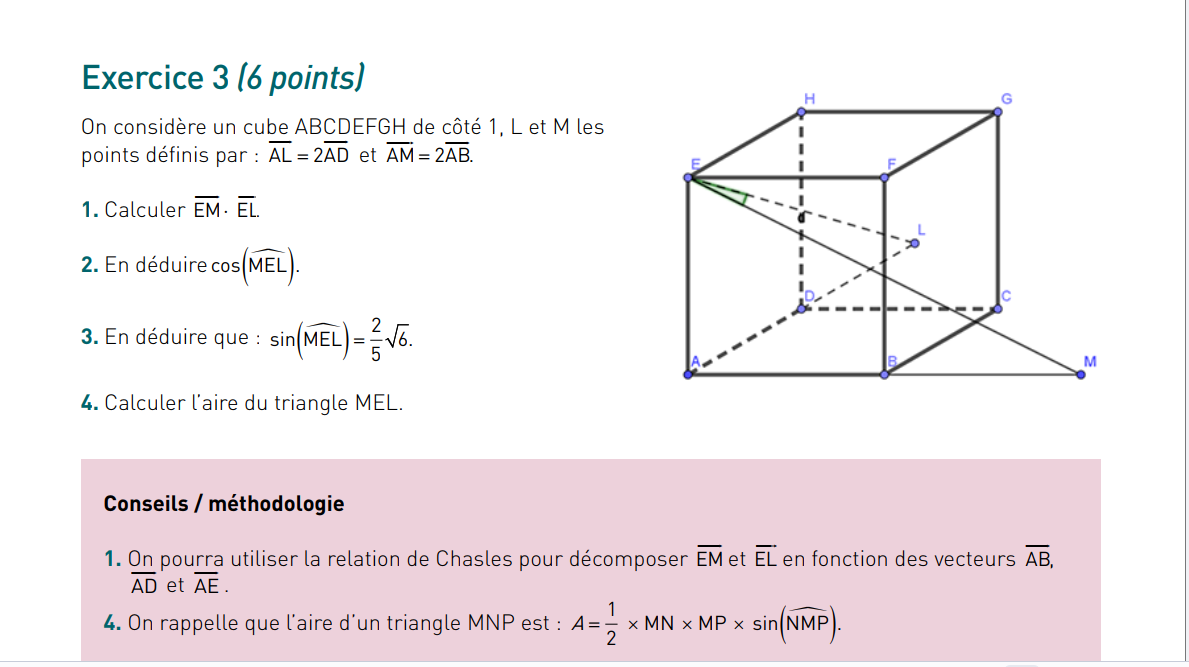

Capture d’écran 2024-07-25 074453.png

Bonjour,

"Juste savoir s'il est possible de le faire"

La réponse est OUI.

Ecris donc ce que tu as fait et il y aura bien un ou l'autre pour t'aider à corriger.

Merci beaucoup pour la réponse;

Je vais mettre ce que j'ai trouvé parce que la je bloque totalement

1 Sachant que (Vecteur EM) = (Vecteur EA) + Vecteur ( AM) = (Vecteur EA) + 2*(Vecteur AB) = 2*(Vecteur AB) - (Vecteur AE)
Alors la norme du ( Vecteur EM) = 2AB-AE; sachant que tous les côté valent 1 alors: ( Vecteur EM) = 21-1 = 1, la norme est donc de 1.
J'ai trouvé la meme chose pour le (Vecteur EL) , ce qui je crois est plutot normal

Ensuite on fait un produit scalaire avec les normes donc selon la formule:

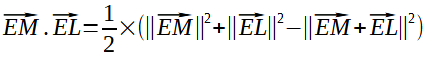
Ce qui donne un résultat de 1.

Et c'est pour la question 2 que je bloque; parce que si le produit scalaire est de 1 on est déduit que cos(MEL) est de 1 ce qui ne fait pas sin(MEL) =

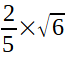
Or si on fait le chemin inverse c'est à dire 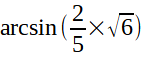, on trouve un angle de 78,46 et des poussière; puis on fait . Ce qui donne 0,2:

Et donc après on revient bien sur l'affirmation de la question 3; sauf que si on fait le calcul du produit scalaire mais avec un angle; je trouve un résultat de 0,2 et non de 1 et là je bloque total.

Voilà ce que j'ai trouvé si quelqu'un peut m'aider à comprendre, je serais content.

Merci d'avance pour vos réponse

Bonjour,

$EM→=EA→+AM→=EA→+2AB→\overrightarrow{EM} = \overrightarrow{EA} + \overrightarrow{AM} = \overrightarrow{EA} + 2 \overrightarrow{AB}$
$EL→=EA→+AL→=EA→+2AD→\overrightarrow{EL} = \overrightarrow{EA} + \overrightarrow{AL} = \overrightarrow{EA} + 2 \overrightarrow{AD}$

$EM→.EL→=EA2+2.EA→.AD→+2.EA→.AB→+4.AB→.AD→\overrightarrow{EM} .\overrightarrow{EL} = EA^2 + 2.\overrightarrow{EA}.\overrightarrow{AD} + 2.\overrightarrow{EA}.\overrightarrow{AB} + 4.\overrightarrow{AB}.\overrightarrow{AD}$

Or $2.EA→.AD→+2.EA→.AB→+4.AB→.AD→=02.\overrightarrow{EA}.\overrightarrow{AD} + 2.\overrightarrow{EA}.\overrightarrow{AB} + 4.\overrightarrow{AB}.\overrightarrow{AD}=0$ (cotés du cubes perpendiculaires) et donc :

$EM→.EL→=EA2=1\overrightarrow{EM} .\overrightarrow{EL} = EA^2 = 1$

On a aussi : $EM→.EL→=∣EM∣.∣EL∣.cos(MEL^)\overrightarrow{EM} .\overrightarrow{EL} = |EM|.|EL|.cos(\hat{MEL} )$
avec $\sqrt{5}$ (Pythagore dans le triangle EAM)
et $\sqrt{5}$ (Pythagore dans le triangle EAL)

Donc : $1=5.5.cos(MEL^)1 = \sqrt{5}.\sqrt{5}.cos(\hat{MEL})$
$cos(MEL^)=15cos(\hat{MEL}) = \frac{1}{5}$

$cos2(MEL^)+sin2(MEL^)=1cos^2(\hat{MEL}) + sin^2(\hat{MEL}) = 1$
$sin2(MEL^)=1−152=2425sin^2(\hat{MEL}) = 1 - \frac{1}{5}^2 = \frac{24}{25}$
$sin2(MEL^)sin^2(\hat{MEL})$ > 0 (angle aigu) $→\to$
$sin(MEL^)=2425=256sin(\hat{MEL}) = \sqrt{\frac{24}{25}} = \frac{2}{5}\sqrt{6}$

$MEL=15.∣EM∣.∣EL∣.sin(MEL^)Aire\ MEL = \frac{1}{5}.|EM|.|EL|.sin(\hat{MEL})$

$MEL=12.5.5.256=6Aire\ MEL = \frac{1}{2}.\sqrt{5}.\sqrt{5}.\frac{2}{5}\sqrt{6} = \sqrt{6}$

Sans relecture de ma part.