Déterminer un nombre de solutions d'une équation selon une valeur k
-
Christophe Christophe dernière édition par
Bonjour à tous,
voici mon problème du jour :
ENONCE
L'objectif de cet exercice est de dénombrer le nombre de solutions de l'équation
2x3+3x²+1=k2x^3+3x²+1=k2x3+3x²+1=k
.
On considère la fonction définie sur R\RR par f(x)=2x3+3x²+1f(x)=2x^3+3x²+1f(x)=2x3+3x²+1
.-
Déterminer f′(x)f'(x)f′(x) et dresser le tableau de variations de fff
-
Déterminer les limites de fff en +∞ et −∞
-
Démontrer que l'équation 2x3+3x²+1=02x^3+3x²+1=02x3+3x²+1=0 admet sur R\RR une unique solution α
Déterminer un encadrement de α à 10−110^{-1}10−1 près. -
Démontrer que l'équation 2x3+3x²=12x^3+3x²=12x3+3x²=1 admet exactement 2 solutions sur R\RR
-
Déterminer le nombre de solutions de l'équation f(x)=kf(x)=kf(x)=k selon les valeurs de k
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−--------------------------------−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
.
Mon travailAucune difficulté pour 1, 2 3 et 4 en utilisant le corollaire du théorème des valeurs intermédiaires.
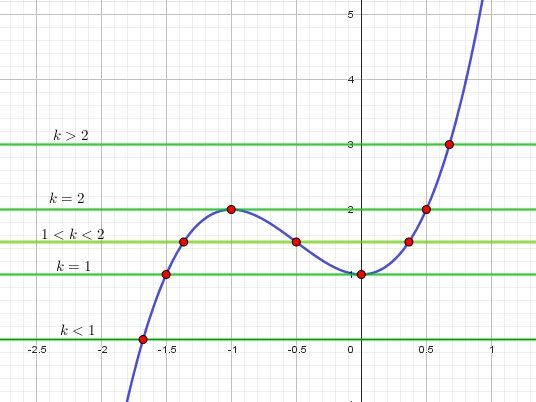
Pour la question 5 en utilisant une lecture graphique je trouve :- 1 solution pour k<1k\lt1k<1 et k>2k\gt2k>2
-
2 solution pour k=1k=1k=1 et k=2k=2k=2
-
3 solutions pour 1<k<21\lt k\lt 21<k<2
Par contre je n'arrive pas à le démontrer
 ... J'imagine qu'il faut utiliser le tableau de variations de fff mais bon je bloque d'où l'appel à un ami
... J'imagine qu'il faut utiliser le tableau de variations de fff mais bon je bloque d'où l'appel à un ami 
Merci par avance

-
-
@Christophe-Christophe Bonsoir,
Oui, il faut utiliser le tableau de variations.
f(x)f(x)f(x) varie de −∞-\infty−∞ à 222, puis de 222 à 111 puis de 111 à +∞+\infty+∞.
Si tu analyses les intervalles, tu peux en déduire le résultat que tu as écrit.
-
Christophe Christophe dernière édition par
Bonjour @Noemi,
merci pour ta réponse... Malheureusement j'avais bien déja tenté d'analyser c tableau de variations .. Malheureusement je n'arrive pas à justifier ma réponse

-
L'intervalle −∞-\infty−∞ à 2 peut se décomposer comme l'union de l'intervalle ∞\infty∞ ; 111 avec l'intervalle 111 ; 222.
L'intervalle 111 à −∞-\infty−∞ peut se décomposer comme l'union de l'intervalle 111 ; 222 avec l'intervalle 111 ; +∞+\infty+∞ donc l'intervalle 111 ; 222 est ....
-
Christophe Christophe dernière édition par
sincèrement désolé @Noemi ... j'imagine que ça doit être tout con mais franchement je me casse la tête mais je n'arrive pas à accoucher de la solution

-
Analyse les trois intervalles : ]−∞;2[]-\infty ; 2[]−∞;2[ ; ]1;2[]1 ; 2[]1;2[ ; ]1;+∞[]1;+\infty[]1;+∞[
Quelle est l'intersection ?
-
Christophe Christophe dernière édition par
Bonjour @Noemi,
pour répondre à ta question l'intersection est ]1;2[]1 ; 2[]1;2[
-
Christophe Christophe dernière édition par Christophe Christophe
en fait je suis en train de voir une chose dans l'énoncé ...
Il est marqué "déterminer" du coup ce n'est pas "démontrer" ? Du coup une simple lecture graphique c'est suffisant pour répondre à la question posée ??Malgré tout, j'aimerais tout de même savoir comment faire pour démontrer ces réponses ... Je buggue

Par ailleurs, les exercices étant souvent guidés, j'imagine qu'il faille faire un lien entre la question 4 et la 5 ... Mais quel est ce lien ?
Vraiment désolé de poser des questions qui doivent vous sembler bien simples mais parfois je me noie dans un verre d'eau

-
Christophe Christophe dernière édition par
est-ce que ce serait tricher de faire ainsi :
- tracer la courbe représentative de fff
- tracer la droite d'équation y=ky=ky=k qui serait la réprésentation d'une fonction ggg
Puis de constater quand il y a intersection entre les 2 ce qui correspond à f(x)=g(x)f(x)=g(x)f(x)=g(x) ?
-
BBlack-Jack dernière édition par
Bonjour,
f(x) = 2x³ + 3x² + 1
f'(x) = 6x² + 6x = 6x(x+1)f'(x) > 0 pour x compris dans ]-oo ; -1] --> f est croissante
f'(x) = 0 pour x =-1
f'(x) < 0 pour x compris dans ]-1 ; 0[ --> f est décroissante
f'(x) = 0 pour x = 0
f'(x) > 0 pour x compris dans ]1 ; +oo[ --> f est croissante.f a un max pour x = -1, ce max vaut f(-1) = 2
f a un min pour x = 0, ce min faut f(0) = 1lim(x--> -oo) f(x) = -oo
lim(x--> +oo) f(x) = +oo
f(-2) = -3 < 0Du tableau de variations de f dressé à partir de ce qui précède, on peut conclure que f(x) = 0 a une seule solution alpha et que alpha est compris dans ]-2 ; -1[
on peut approcher la valeur de alpha par approximations successives, par exemple par dichotomie ... et on trouve que alpha est compris dans ]-1,6 ; -1,7[On a alors, le tableau de variations complété :
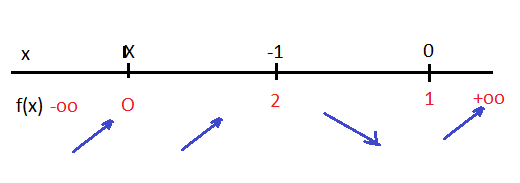
A partir de la lecture de ce tableau, on peut soit (avec un brin de réflexion) en déduire directement le nombre de solutions de f(x) = k (en fonction de la valeur de k)
Soit, on peut tracer grossièrement l'allure du graphe de f(x) en respectant le tableaux de variations ... et, de ce graphe, déduire le nombre de solutions de f(x) = k (en fonction de la valeur de k)
-
Oui la réponse en utilisant le tracé de la droite y=ky=ky=k est correcte.
L'intersection sur les trois intervalles est bien ]1;2[]1;2[]1;2[, donc trois solutions sur cet intervalle.
-
mtschoon dernière édition par mtschoon

Bonjour à tous,
Lecture graphique pour la question 5)
La représentation graphique de f est en bleu
Les droites d'équation y=k, suivant k, sont en vert
Les solutions de l'équation f(x)=k, suivant k, sont les abscisses des points en rouge.
Les conditions sur k sont écrites au dessus des droites (5 cas)