limite d'une suite définie par récurrenc

Bonjour à tous,

je suis bloqué à la dernière question d'un problème.

Qqs données de l'énoncé

$f (x) = l n (x ² + 4)$
$g (x) = f (x) - x$

$u_0=0$
$u_{n+1}=f(u_n)$
Les questions précédentes m'ont conduit à démontré que la suite $0≤un≤α0\le u_n \le \alpha$ et est strictement croissante et dc qu'elle converge vers une limite $l$ .

Je cherche à démontrer que $l=αl=\alpha$

Je sais que lim de $u_n$ quand n tend vers $\infin$ = $l$
et que que lim de $u_{n+1}$ quand n tend vers $\infin$ = $l$

Mais après je suis bloqué ... Grrr

Je suis donc preneur de vos précieux conseils
Merci par avance

Bonjour,

Ce n'est pas parce la suite est croissante et que alpha est un majorant que la limite L vers où la suite converge est alpha.

La suite converge ... et on sait que L <= alpha.

On peut cependant trouver la valeur de L.

Quand on a démontré que la suite convergeait ...

Soit L la valeur vers ou la suite converge.

On a :
lim(n-->+oo) U(n) = L
lim(n-->+oo) U(n+1) = L

Et donc par la relation de récurrence : L = ln(L² + 4)

Relation de laquelle on peut tirer L (mais ce n'est pas immédiat et pas accessible par des fonctions usuelles)

On peut aussi le faire en étudiant la fonction f(x) = x - ln(x²+4) et approcher au final avec la précision qu'on veut, mais pas la valeur exacte de L, par approximations successives.

On trouve L = 2,1587...

Bonjour @Black-Jack et merci tardif pour ta réponse

Bonjour,

@Christophe-Christophe

Tu n'as pas tout dit sur cette valeur $α\alpha$ que tu as dû trouver dans une question précédente de ton énoncé et que tu ne donnes pas ici...

J'imagine que l'énoncé t'a demandé d'étudier la fonction $g$
définie par $g(x)=f(x)-x=ln(x^2+4)-x$
Après étude, g est continue, strictement décroissante, donc bijective , de $R$ vers $R$ .
Tout élément de $R$ (ensemble d'arrivée) à un antécédent unique dans l'ensemble de départ ( $R$ ).
En particulier, $0$ de l'ensemble d'arrivée a un antécédent unique $α\alpha$ dans l'ensemble de départ.
(Tu peux aussi utiliser le TVI)
Il existe un réel $α\alpha$ unique tel que $g(α)=0\boxed{g(\alpha)=0}$
(A la calculette $α≈2.16)\alpha\approx 2.16)$
$g(α)=0g(\alpha)=0$ <=> $f(α)−α=0f(\alpha)-\alpha=0$ <=> $f(α)=α\boxed{f(\alpha)=\alpha}$

Ainsi, la conclusion sur la limite de la suite $U_n)$ est immédiate.

Après avoir prouver la convergence de la suite $U_n)$ définie par $U_{n+1}=f(U_n)$ , la limite $L$ satisfait à : $L = f (L)$ c'est à dire $f(L)=L\fbox{f(L)=L}$

Vu que l'équation $f (x) = x$ a une solution réelle unique $α\alpha$ , nécessairement $L=α\boxed{L=\alpha}$

CQFD

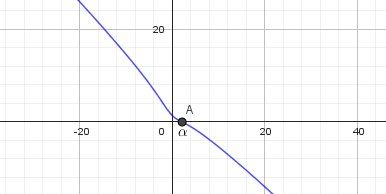
Représentation graphique de $g$ définie par :
$g(x)=f(x)-x=ln(x^2+4)-x$