Recherche de l'équation d'une fonction exponentielle

Demandé de correction exercice
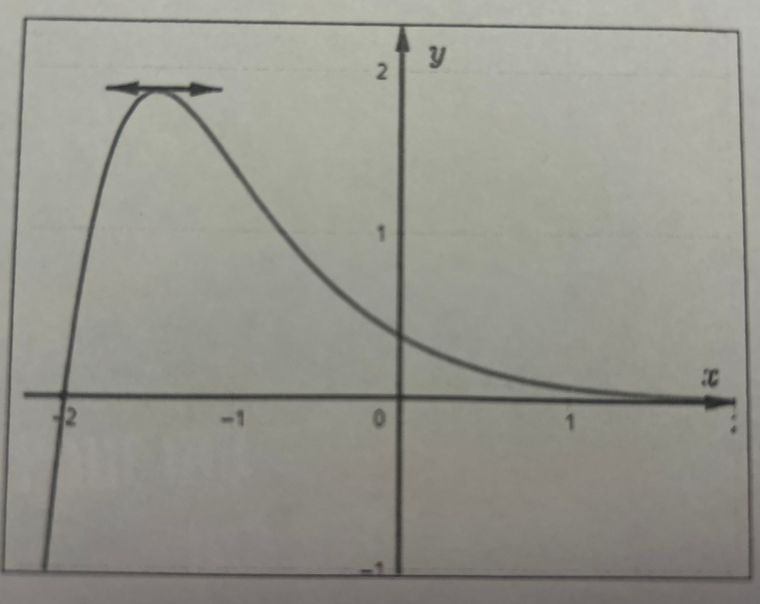
Bonjour, c’était pour vous demandez si les réponses sont corrects je vous remercie,

La courbe (C) ci-contre est celle d'une fonction f, définie et dérivable sur IR.
On sait que le point A(3-/;exp^2/4) est sur (C) et que la tangente à (C) en A est parallèle à l'axe des abscisses.
De plus, pour tout réel x, on a :
équat. cn
f(x) = (ax + b)e^ -2x-1
où a et b sont deux réels fixés.

Calculer une expression f' (x) de la dérivée de fen fonction des réels a et b.
Déterminer les réels a et b : justifier.

Réponses :

La fonction donnée est :
f(x) = (ax + 6) e-2x-1
Pour calculer la dérivée f' (x), nous allons utiliser la règle du produit. Soit
и (x) = ax + b et v (x) = e 2x-1. La dérivée de f est donnée par :
f' (x) = ' (x) 0(x) + 4(x) 0(x)
Calculons chaque dérivée :- u' (x) = a

Pour v (x) = e-2x-1, nous avons
v' (x) = - 2e-2x-1 (en utilisant la
règle de la chaîne). En remplaçant dans la formule de la dérivée, nous avons :
f' (x) = a • e-22-1 + (ax + 6) (-2e-2x-1)
En simplifiant :
f' (x) = ae-2x-1 - 2(ax + 6)e-2x-1
En regroupant les termes :
f' (x) = e 2x-1 (a - 2(ax + 6)) = e 2x-1(a
Finalement, l'expression de la dérivée est :
f' (x) = e-2x-1(-2ax + a - 26)

(f)´(3-/2) = e^2(-2a(3-/2) + a -2b)
On doit avoir :
4a - 26 = 0 …

@hiba_mrcnn Bonsoir,

D'ou vient le $6$ dans la dérivée ?
La dérivée est $f'(x)= (-2ax+a-2b)e^{-2x-1}$

Pour le calcul de $a$ et $b$ , utilise les coordonnées du point $A$ et la valeur de la dérivée au point de tangence.

Tu dois trouver : $(\frac{1}{2}x+1)e^{-2x-1}$

Indique tes calculs si tu souhaites une vérification.

@Noemi
Je me suis tromper c’est b

@Noemi
Je ne trouve ps le meme calcul je pourrais avoir le détails s’il vous plaît ?

@hiba_mrcnn
Tu utilises les coordonnées du point $(-\dfrac{3}{2} ; \dfrac{e^2}{4})$
qui donne :
$(−32a+b)e3−1=e24(-\dfrac{3}{2}a+b)e^{3-1}= \dfrac{e^2}{4}$ et en simplifiant :

$(−32a+b)=14(-\dfrac{3}{2}a+b)= \dfrac{1}{4}$

Pour l'autre équation, tu utilises le fait que la dérivée est nulle pour $-\dfrac{3}{2}$ .
Soit $3a+a-2b)e^2=0$ , soit $4 a - 2 b = 0$

Il reste à résoudre le système pour déterminer la valeur de $a$ et $b$ .

Indique tes calculs et ou résultats si tu souhaites une vérification.

@Noemi
J’obtiens un système d’équation : 2a =b2
3-/2a + b = 1/4 on remplaçant b par 2 a sa donne
3-/2a + 2a = 1/4
1/2a =1/4 soit a = 1/2

Pour trouver b :
b = 2(1/2) =1

Donc les valeurs de a et b sont :
a = 1/2 ; b= 1

C’est bon pour cette exercice du coup et pour les calculs de la première question ?

@hiba_mrcnn

Attention à ce que tu écris
Première ligne 2a =b2, c'est : $2 a = b$ .
et bizarre l'écriture 3-/2a qui correspond à $−32a-\dfrac{3}{2}a$ .

Pour la première question, j'ai indiqué la réponse. Utilise les formules de calcul de la dérivée.

@Noemi
Oui c’est ça par contre pour l’autre équation je ne comprends ps

@hiba_mrcnn

La question 1. c'est le calcul de la dérivée
$f(x)=(ax+b)e^{-2x-1}$
C'est un produit en prenant :
$u (x) = a x + b$ ; $u^{'} (x) = a$
$v(x)= e^{-2x-1}$ ; $v'(x)= -2e^{-2x-1}$
ensuite tu appliques :
la dérivée de $u(x)×v(x)u(x)\times v(x)$ est $u^{'} (x) v (x) + u (x) v^{'} (x)$

Indique tes calculs et/ou résultats si tu souhaites une vérification.

@Noemi

Cela donne donc :

@hiba_mrcnn

Des erreurs dans ce que tu as écrit.

La question 1. c'est le calcul de la dérivée
$f(x)=(ax+b)e^{−2x−1}$
C'est un produit en prenant :
$u (x) = a x + b$ ; $u^{'} (x) = a$
et
$v(x)=e^{−2x−1}$ ; $v'(x)= -2e^{-2x-1}$

ensuite tu appliques la dérivée de $u(x)×v(x)u(x)\times v(x)$ qui est : $u^{'} (x) v (x) + u (x) v^{'} (x)$

Donc $f'(x)= ae^{-2x-1}+(ax+b)(-2e^{-2x-1})$
$f'(x)= (a-2ax-2b)e^{-2x-1}$
si tu ordonnes :
$f'(x)=(-2ax-a-2b)e^{-2x-1}$

@Noemi

D’accord merci beaucoup je vais faire le 2 faites moi un retour

Ce message a été supprimé !

@Noemi
Voilà le 2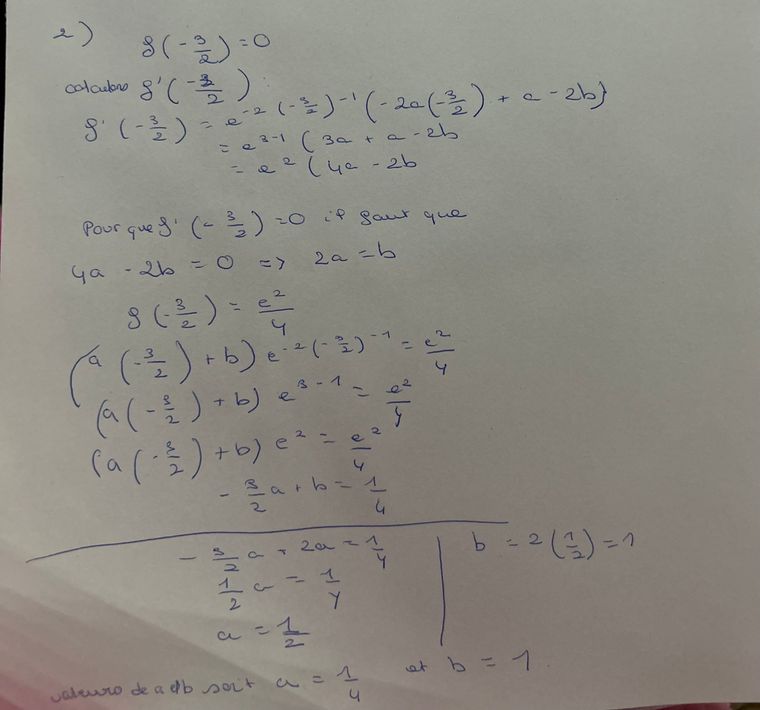

@hiba_mrcnn

Le calcul est juste la conclusion fausse, tu as écrit $\dfrac{1}{4}$ au lieu de $a=12a=\dfrac{1}{2}$ .

@Noemi

Ah oui sa serai possible d’avoir la correction avec des phrases s’il vous plaît ?

@hiba_mrcnn
On utilise les coordonnées du point $(-\dfrac{3}{2} ; \dfrac{e^2}{4})$
$(−32a+b)e3−1=e24(-\dfrac{3}{2}a+b)e^{3-1}= \dfrac{e^2}{4}$ et en divisant l'équation par $e^2$ :

$(−32a+b)=14(-\dfrac{3}{2}a+b)= \dfrac{1}{4}$

On utilise le fait que la dérivée est nulle pour $-\dfrac{3}{2}$ car la tangente est horizontale .
$3a+a-2b)e^2=0$ , soit $4 a - 2 b = 0$ donc $2 a - b = 0$

on écrit le système pour déterminer la valeur de $a$ et de $b$ .
$(2)\begin{dcases} (-\dfrac{3}{2}a+b)= \dfrac{1}{4} \ (1)\cr2a-b=0 \ (2) \end{dcases}$
De l'équation $(2)$ , on déduit $b = 2 a$ que l'on remplace dans l'équation $(1)$
ce qui donne : $−32a+2a=14-\dfrac{3}{2}a+2a= \dfrac{1}{4}$
Soit $12a=14\dfrac{1}{2}a=\dfrac{1}{4}$ , donc $a=12a=\dfrac{1}{2}$

On remplace $a$ par $12\dfrac{1}{2}$ dans l'équation $(2)$
Soit $1 - b = 0$ donc $b = 1$ .
Conclusion $a=12a=\dfrac{1}{2}$ et $b = 1$

@Noemi

Ah d’accord merci beaucoup