Variations de fonctions et suite

Ce message a été supprimé !

Question 1 : Si $g(x)= 3e^{2x}-2e^{3x}+1$
$g'(x)= 6e^{2x}-6e^{3x}$
soit en factorisant
$g'(x)=6e^{2x}(1-e^x)$
Il reste à résoudre $\geq 0$ et la question b.

Question 2 : $f(x)=x2x+1f(x)=\dfrac {x}{2x+1}$

La dérivée : $\dfrac{2x+1-x\times2}{(2x+1)^2}= ....$

je te laisse poursuivre les calculs. Indique tes calculs et/ou résultats si tu souhaites une vérification.

Ce message a été supprimé !

@hiba_mrcnn

Reprends l'exercice dans l'ordre, question par question.
Tu indiques au début : Supposons que alors que c'est une donnée de l'énoncé.

@Noemi
Je comprends ps je peux avoir le corriger directement ?

@hiba_mrcnn

Question 1 a. : Commence par résoudre : $\geq 0$ .

Ce message a été supprimé !

Ce message a été supprimé !

@hiba_mrcnn

La fonction $g$ n'est pas celle que j'ai écrit dans ma première réponse ?
Est ce que $g(x) = 3e^{2x}-2e^{3x+1}$ ?

Dans ce cas vérifie la dernière ligne de ton calcul de dérivée.

Ce message a été supprimé !

@hiba_mrcnn

Je reprends ma question :
$g(x) = 3e^{2x}-2e^{3x+1}$
ou
$g(x)= 3e^{2x}-2e^{3x}+1$

Quelle est la bonne écriture, la première ou la deuxième ?

@Noemi
Première

@hiba_mrcnn

Donc la dérivée est : $g'(x)=6e^{2x}-6e^{3x+1}$
si on factorise $g'(x)=6e^{2x}(1-e^{x+1})$
Pour la résolution de l'inéquation : $g′(x)≥0g'(x)\geq 0$
il faut résoudre $1−ex+1≥01-e^{x+1}\geq0$
soit $ex+1≤1e^{x+1}\leq1$
soit $x+1≤0x+1\leq0$

Ce message a été supprimé !

@hiba_mrcnn

Non, Consulte ma réponse.

@Noemi
Oui mais vous vous êtes trompez sur le début de dérivée pouvant nous reprendre du tout début s’il vous plaît

@Noemi
Sachant que l’on doit dérivée g(x) = 3e^2x - 2e^3x+1

@hiba_mrcnn

Oui, on peut reprendre des le début.
A la question :
Quelle est la bonne écriture de la fonction, la première ou la deuxième ?
$g(x) = 3e^{2x}-2e^{3x+1}$
ou
$g(x)= 3e^{2x}-2e^{3x}+1$

Tu as répondu : la première,
donc
$g(x) = 3e^{2x}-2e^{3x+1}$

Est-ce exact ?

@Noemi
Oui jusqu’à la

@hiba_mrcnn

Avec $g(x) = 3e^{2x}-2e^{3x+1}$
la dérivée : $g'(x)= 6e^{2x}-6e^{3x+1}$
On factorise $6e^{2x}$
$g'(x)=6e^{2x}(1-e^{x+1})$

Résoudre l'inéquation $g′(x)≥0g'(x)\geq 0$ revient à résoudre l'inéquation :
$1−ex+1≥01-e^{x+1}\geq0$ car $e2x>0e^{2x} \gt0$

pour $1−ex+1≥01-e^{x+1}\geq0$ équivalent à
$ex+1≤1e^{x+1}\leq1$ soit $x+1≤0x+1\leq 0$ ou $x≤−1x\leq -1$ .

@Noemi

Ah oui je vois

@Noemi
Donc il va falloir faire le tableau de variation par la suite ?

@hiba_mrcnn

Oui, fais le tableau de variation.

@Noemi
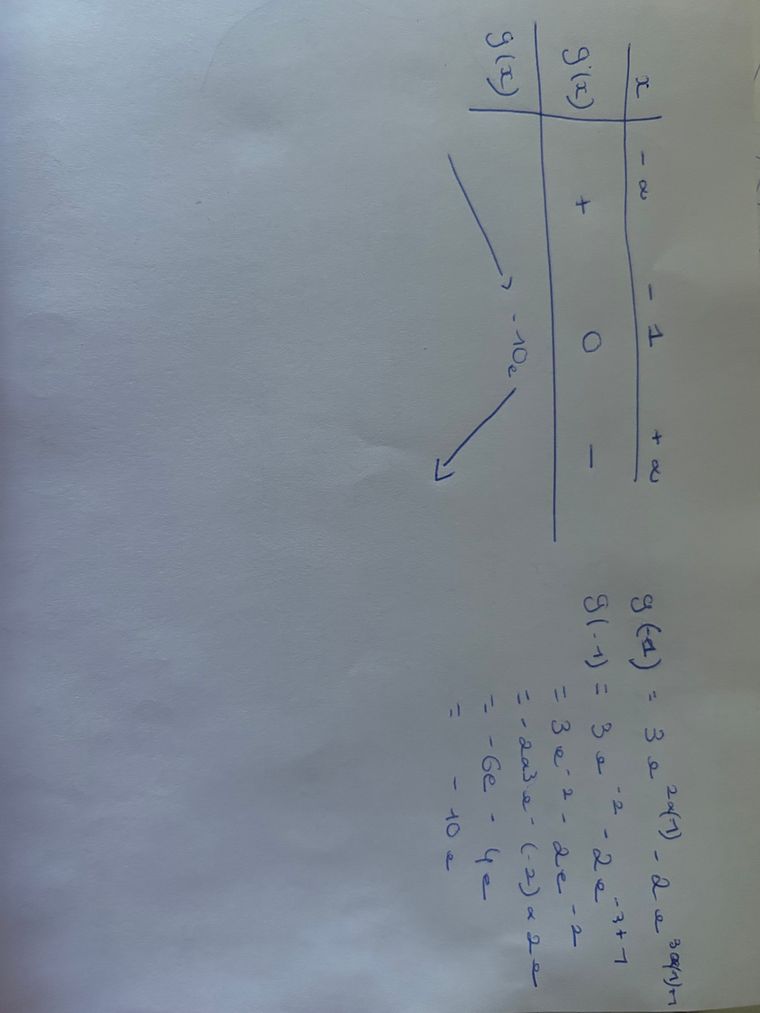
Cela donne donc :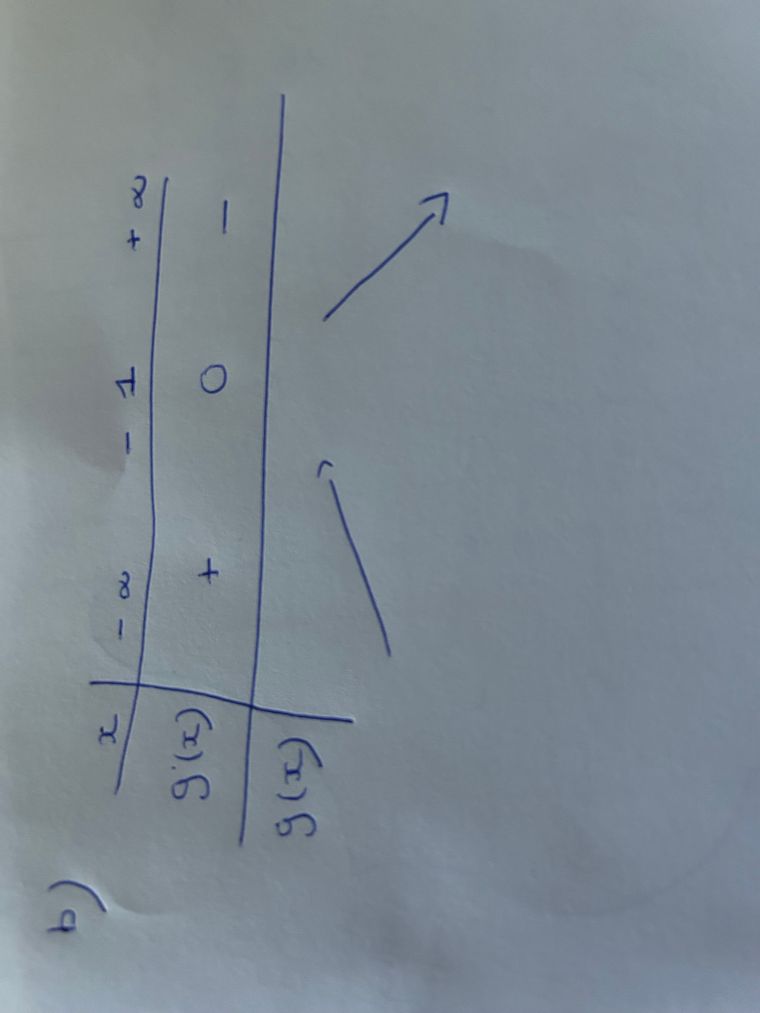

@hiba_mrcnn

Oui, mais il manque les limites pour la fonction $g$ .

@Noemi
Je remplace les X par -1 ?

@hiba_mrcnn

Oui pour $g (- 1)$ .

@Noemi

@hiba_mrcnn

Le début est juste mais la fin fausse.
$g(-1)=3e^{-2}-2e^{-2}$
$g(-1)=e^{-2}(3-2)$
$g(-1)=e^{-2}$

@Noemi

Merci du coup le rustre pour c’est deux questions donne ?

@hiba_mrcnn

Pour le tableau de variation, il manque les limites en $−∞-\infty$ et en $+∞+\infty$ si ton professeur les demandes.
Si non la question 1 est terminée.

@Noemi

Vous pouvez résumer les 2 questions s’il vous plaît

@hiba_mrcnn

a. Calcul de la dérivée :
$g(x) = 3e^{2x}-2e^{3x+1}$
la dérivée : $g'(x)= 6e^{2x}-6e^{3x+1}$
On factorise $6e^{2x}$
$g'(x)=6e^{2x}(1-e^{x+1})$

Résolution de l'inéquation $g′(x)≥0g'(x)\geq 0$
Cela revient à résoudre l'inéquation :
$1−ex+1≥01-e^{x+1}\geq0$ car $e2x>0e^{2x} \gt0$ pour tout $x$ .

$1−ex+1≥01-e^{x+1}\geq0$ équivalent à
$ex+1≤1e^{x+1}\leq1$ ; $ln(ex+1)≤ln1ln(e^{x+1})\leq ln1$ soit $x+1≤0x+1\leq 0$ ou $x≤−1x\leq -1$ .

b. Variations de la fonction :
Pour $\lt -1$ , $g′(x)>0g'(x)\gt0$ donc la fonction est croissante.
Pour $\gt -1$ , $g′(x)<0g'(x)\lt0$ donc la fonction est décroissante.
pour $x = - 1$ $g^{'} (x) = 0$ et $g(-1)=3e^{-2}-2e^{-2}=e^{-2}$
Tableau de variations
.... a compléter.

@Noemi

Le tableau de variation il y’a juste le e^-2 que je dois placer à la place du 10 et le - infini et plus infini sur les flèches ?

@Noemi

Comme cela

@hiba_mrcnn

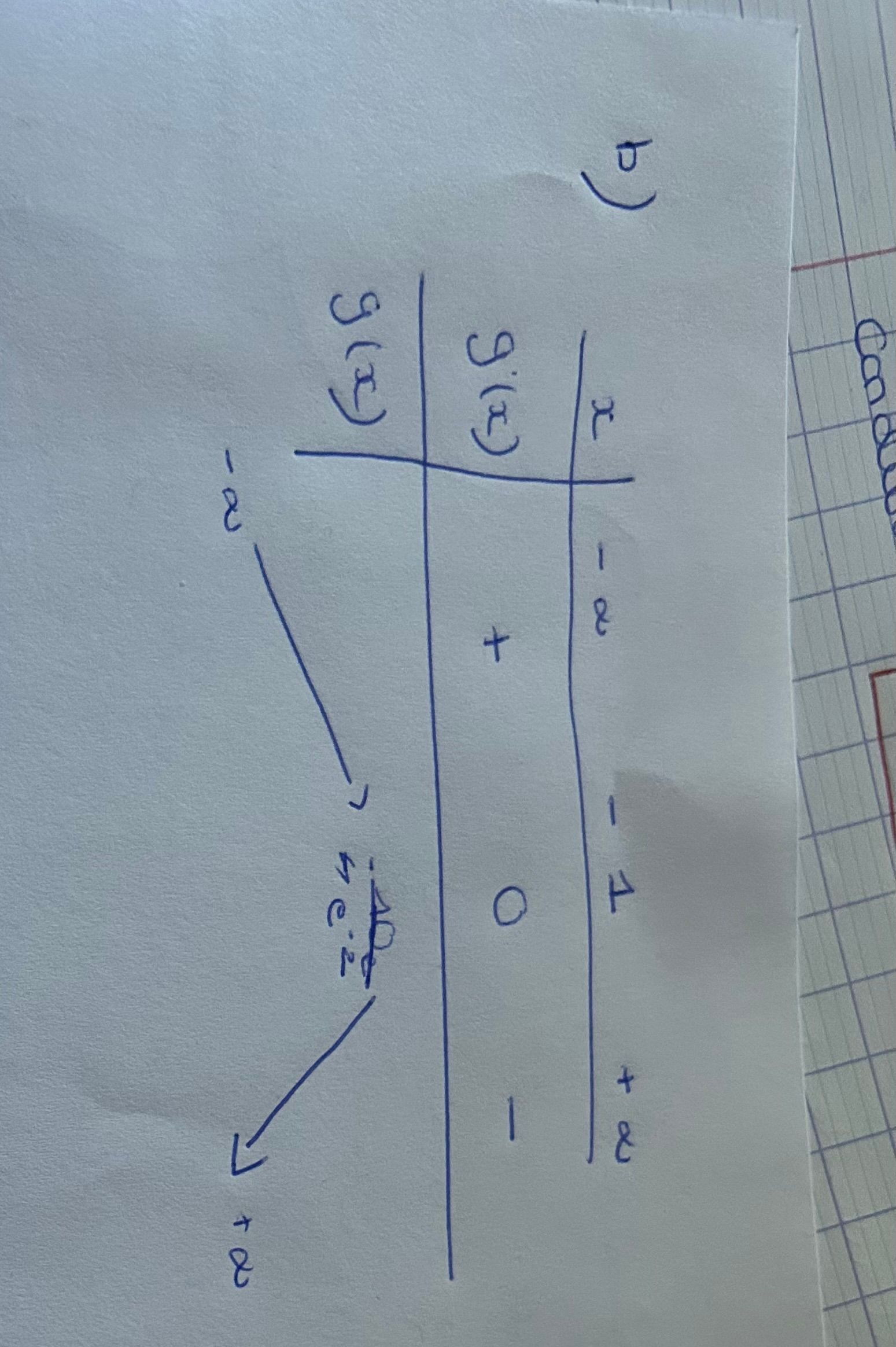
Les limites sont fausses :
à gauche $0^+$ et à droite $−∞-\infty$ .

@Noemi
Comme ceci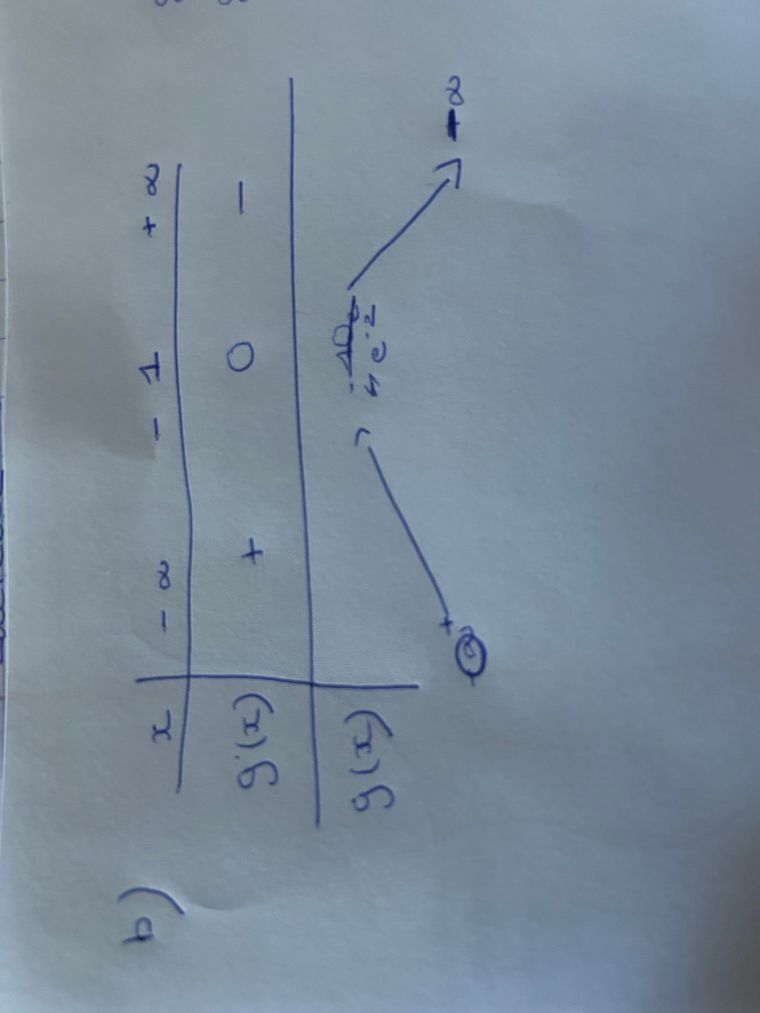

@hiba_mrcnn

Oui, c'est correct.

Ce message a été supprimé !

@Noemi

D’accord merci beaucoup maintenant pour la dernière partie qui est

Soit (un) la suite définie par uo = 3, et, pour tout entier naturel n, Un+1 = Un/2un+1
a. Soit f (x) = x/2x+1 : montrer que la fonction f est croissante sur l'intervalle [0; + infini [.
b. Soitn un entier naturel tel que 0 ≤ Un+1 ≤ Un : justifier le fait que l'on a alors 0 ≤ Un+2 ≤ Un+1•
c. En raisonnant par récurrence, démontrer que la suite (un) est décroissante et minorée par 0.

Les réponses : cela est bon ?

@hiba_mrcnn

Pour la question a. simplifier l'expression de la dérivée et indique le signe du numérateur.

@hiba_mrcnn

On sait que $\leq U_{n+1} \leq U_n$ . Puisque $U_{n+1}$ est un entier naturel, cela implique que $Un+1≥0U_{n+1} \geq 0$ .

On étudie $U_{n+2}$ . Comme $\leq U_{n+1} \leq U_n$ , nous avons deux cas à examiner :

Si $Un+1>0U_{n+1} \gt 0$ , alors $U_{n+2}$ est également un entier naturel tel que $\leq U_{n+2} \leq U_{n+1}$ .
Si $U_{n+1} = 0$ , alors $Un+2≥0U_{n+2} \geq 0$ et $Un+2≤Un+1=0U_{n+2} \leq U_{n+1} = 0$ , donc $U_{n+2} = 0$ .

Donc $\leq U_{n+2} \leq U_{n+1}$ .

@Noemi

Comme ça ?

@hiba_mrcnn

Oui pour la simplification de la dérivée.

Pour la question b.

On sait que $\leq U_{n+1} \leq U_n$ . Puisque $U_{n+1}$ est un entier naturel, cela implique que $Un+1≥0U_{n+1} \geq 0$ .

On étudie $U_{n+2}$ . Comme $\leq U_{n+1} \leq U_n$ , nous avons deux cas à examiner :

Si $Un+1>0U_{n+1} \gt 0$ , alors $U_{n+2}$ est également un entier naturel tel que $\leq U_{n+2} \leq U_{n+1}$ .
Si $U_{n+1} = 0$ , alors $Un+2≥0U_{n+2} \geq 0$ et $Un+2≤Un+1=0U_{n+2} \leq U_{n+1} = 0$ , donc $U_{n+2} = 0$ .

Donc $\leq U_{n+2} \leq U_{n+1}$ .

Pour la question c.

Initialisation : Pour $n = 0$ , comme $U_0=3$ qui est un entier naturel positif. Donc, $U_n)$ est bien minoré par 0.

Hérédité : On suppose que pour un entier $k$ , $Uk≥Uk+1≥0U_k \geq U_{k+1} \geq 0$ . il faut démontrer que cela implique que $Uk+1≥Uk+2≥0U_{k+1} \geq U_{k+2} \geq 0$ .

Comme $Uk≥Uk+1U_k \geq U_{k+1}$ , cela implique que $Uk+1≥Uk+2U_{k+1} \geq U_{k+2}$ .

Ainsi, nous avons $Uk+1≥Uk+2U_{k+1} \geq U_{k+2}$ et $Uk+2≥0U_{k+2} \geq 0$ .

Donc pour tout entier $n$ , $Un≥Un+1≥0U_n \geq U_{n+1} \geq 0$ , donc la suite $U_n)$ est décroissante et minorée par 0.

@Noemi

Ah d’accord je pourrais avoir le résumer avec les phrases s’il vous plaît, on indiquant les erreurs ?

@hiba_mrcnn

Pour la a

@hiba_mrcnn

Reprend toutes mes réponses, j'ai indiqué des phrases.

@Noemi

Oui merci beaucoup mais je parles de la question A

@hiba_mrcnn

$f(x)=x2x+1f(x)=\dfrac {x}{2x+1}$ la fonction $f$ est définie pour $x$ différent de $−12-\dfrac{1}{2}$

La dérivée : $\dfrac{2x+1-x\times2}{(2x+1)^2}= \dfrac{1}{(2x+1)^2}$
$1>01\gt0$ et $(2x+1)2>0(2x+1)^2\gt0$ donc $f′(x)>0f'(x)\gt0$
la fonction $f$ est donc croissante sur l'intervalle $]−12;+∞[]-\dfrac{1}{2} ; +\infty[$ donc sur l'intervalle $+\infty[$ .

@Noemi

Mercii

@hiba_mrcnn

C'est parfait si tu as tout compris.

Je veux sur oscillations en terminale s

@Lamé-Fofana Bonsoir,

Propose ta question avec précision dans un nouveau sujet.