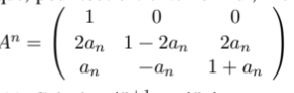calcule de matrice avec suites
-
Jjean 12 dernière édition par jean 12
bonsoir j'ai un exercice sur les matrices que je n'arrive pas à comprendre certaines parties
On considère la matrice: A (voir schéma )
-
Calculer la matrice A^2
-
On définit A^n pour tout n non nul et A^(n+1)=(A^n)×A
a) Calculer A^(n+1)
(b) En déduire la relation: a(indice n+1)=3-2×a(indice n)
- Soit la suite (bn) définie pour tout entier naturel n non nul par: b(indice n) = a(indice n) - 1
(a) Montrer que (bn) est une suite géométrique dont on précisera le premier terme et la raison.
(b) Calculer bn puis an en fonction de n.
- En déduire A^n en fonction de n.
pour la question 1 j'ai trouvé
- A^2= {1 0 0 : -6 7 -6 : -3 3 -2} j'ai mis les deux points pour séparer les différentes lignes
- pour le deuxième j'ai trouvé ( mais je ne suis pas trop sûre de mes résultats)
A^ (n+1)=(1 0 0 : 6-4an -5+7an 6-4an : 3-2an -3+2an 4-2an)
à partir d'ici je n'arrive pas à comprendre la suite de l'exercice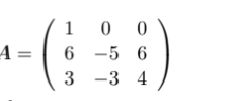
-
-
Jjean 12 dernière édition par
-
@jean-12 Bonjour,
Le calcul de A2A^2A2 est juste.
Vérifie le calcul de An+1A^{n+1}An+1
Tu dois trouver :
(1 0 06−4a 4a−5 6−4a3−2a 2a−3 4−2a)\begin{pmatrix} 1 \ \ \ 0 \ \ \ \ 0 \cr 6-4a \ 4a-5\ 6-4a \cr 3-2a \ 2a-3 \ 4-2a \end{pmatrix}⎝⎜⎛1 0 06−4a 4a−5 6−4a3−2a 2a−3 4−2a⎠⎟⎞
-
Jjean 12 dernière édition par
@Noemi bonsoir
comment faire pour démontrer la relation de la question 2-b
-
Jjean 12 dernière édition par
@Noemi j'ai recalculé et j'ai trouvé le même résultat pour A^(n+1)
-
Jjean 12 dernière édition par
@jean-12 maintenant j'aimerais que vous m'expliquiez la question 2b
-
Ecris la matrice An+1A^{n+1}An+1 en fonction de an+1a_{n+1}an+1 puis tu compares les termes avec la matrice trouvée précédemment.
-
Jjean 12 dernière édition par
@Noemi au fait je n'arrive pas à bien comprendre
-
An+1=(1 0 02an+1 1−2an+1 2an+1an+1 −an+1 1+an+1)A^{n+1}=\begin{pmatrix} 1 \ \ \ 0 \ \ \ \ 0 \cr 2a_{n+1} \ 1-2a_{n+1}\ 2a_{n+1} \cr a_{n+1} \ -a_{n+1}\ 1+a_{n+1} \end{pmatrix}An+1=⎝⎜⎛1 0 02an+1 1−2an+1 2an+1an+1 −an+1 1+an+1⎠⎟⎞
la deuxième ligne donne :
2an+1=6−4an2a_{n+1}=6-4a_n2an+1=6−4an
1−2an+1=4an−51-2a_{n+1}=4a_n-51−2an+1=4an−5
....Tu en déduis an+1=...a_{n+1}= ...an+1=...
-
Jjean 12 dernière édition par
@Noemi vous avez remplacez l'indice n par n+1 et j'aimerais savoir pourquoi vous avez fait ça
-
La matrice AnA^nAn est exprimée en fonction de ana_nan.
La matrice An+1A^{n+1}An+1 a son expression en fonction de an+1a_{n+1}an+1 en remplaçant nnn par n+1n+1n+1
-
Jjean 12 dernière édition par
@Noemi
ahh d'accord je comprends maintenant merci beaucoup
-
C'est parfait. Bonne nuit.
-
Ttyhgtre dernière édition par
Noemi a trop d'égo, il veut toujours montrer que les exercices ont été trouvés grâce à lui. Arrête ça, tu n'es pas le centre de ce site, laisse les autres répondre