Devoir sur un exercice

[hiba_mrcnn]

Bonjour, j’aimerai avoir de l’aide pour l’exercice :

Soit f la fonction définie sur R par : f(x) = x - (x + 1)e^-x.
On admet que f est deux fois dérivable sur R.

1. Montrer que, pour tout réel x, la dérivée de f vérifie : f' (x) = 1 + xe^-x

2. Étude de la dérivée f'.
   a. Calculer les limites de f'en -∞ et en +∞o
   b. Dresser le tableau de variation de f' sur R
   c. Montrer que l'équation f' (x) = 0 admet une unique solution réelle a dont on donnera une valeur approchée à 10^-3 près.
   d. En déduire le signe de f'(x) en fonction de x.

3. A l'aide des questions précédentes :
   a. Montrer que f admet un minimum sur R qui est égal à : a^2 +a+1/a
   b. Étudier la convexité de f sur R: on précisera les coordonnées du point d'inflexion de sa courbe.

[Black-Jack]

Bonjour,

Commence par mettre sur le site ce que tu as réussi à faire.

On pourra alors t'aider à corriger si nécessaire et te donner des pistes pour terminer.

[Noemi]

@hiba_mrcnn Bonjour,

Pour le calcul de la dérivée :
la dérivée de $x$ est $1$
La dérivée de $(x+1)e^{-x}$ forme $U\times V$
soit $1\times e^{-x}-(x+1)e^{-x}=....$

Je te laisse poursuivre le calcul.

[hiba_mrcnn]

@Black-Jack

Oui bonsoir j’ai essayer de faire la première parti

[Noemi]

@hiba_mrcnn

1. La démonstration proposée pour la dérivée est incorrecte.
2. a) le calcul pour les limites est à revoir. L'étude porte sur la fonction dérivée.

[hiba_mrcnn]

@Noemi

Hein mais la dérivée c’est bien ça

[hiba_mrcnn]

@Black-Jack

Erreur v’(x) = e^-x

Donc, [ (x+1)e^{-x})' = (1)e^{-x} + (x+1)(-e^{-x}) = e^{-x} - (x+1)e^{-x} = e^{-x} - xe^{-x} - e^{-x} ]

[Noemi]

@hiba_mrcnn

Le résultat est correct mais la démonstration non.
Si tu poses $u(x)$ et $v(x)$ précise le calcul de $u^{\prime }(x)$ et $v^{\prime }(x)$
Si tu calcules directement cela donne :
$f(x)=x-(x+1)e^{-x}$
$f^{\prime }(x)=1-[1\times e^{-x}+(x+1)\times (-e^{-x})]$
$f^{\prime }(x)=1-[e^{-x}-x{e}^{-x}-e^{-x}]$
soit
$f^{\prime }(x)=1+x{e}^{-x}$
Pour les limites, détaille le calcul des limites de $x{e}^{-x}$

[hiba_mrcnn]

@Noemi

Ah je comprends mieux je vous mets ce que j’ai afin de pouvoir avoir une correction détaillée je vous remercie

[Noemi]

@hiba_mrcnn

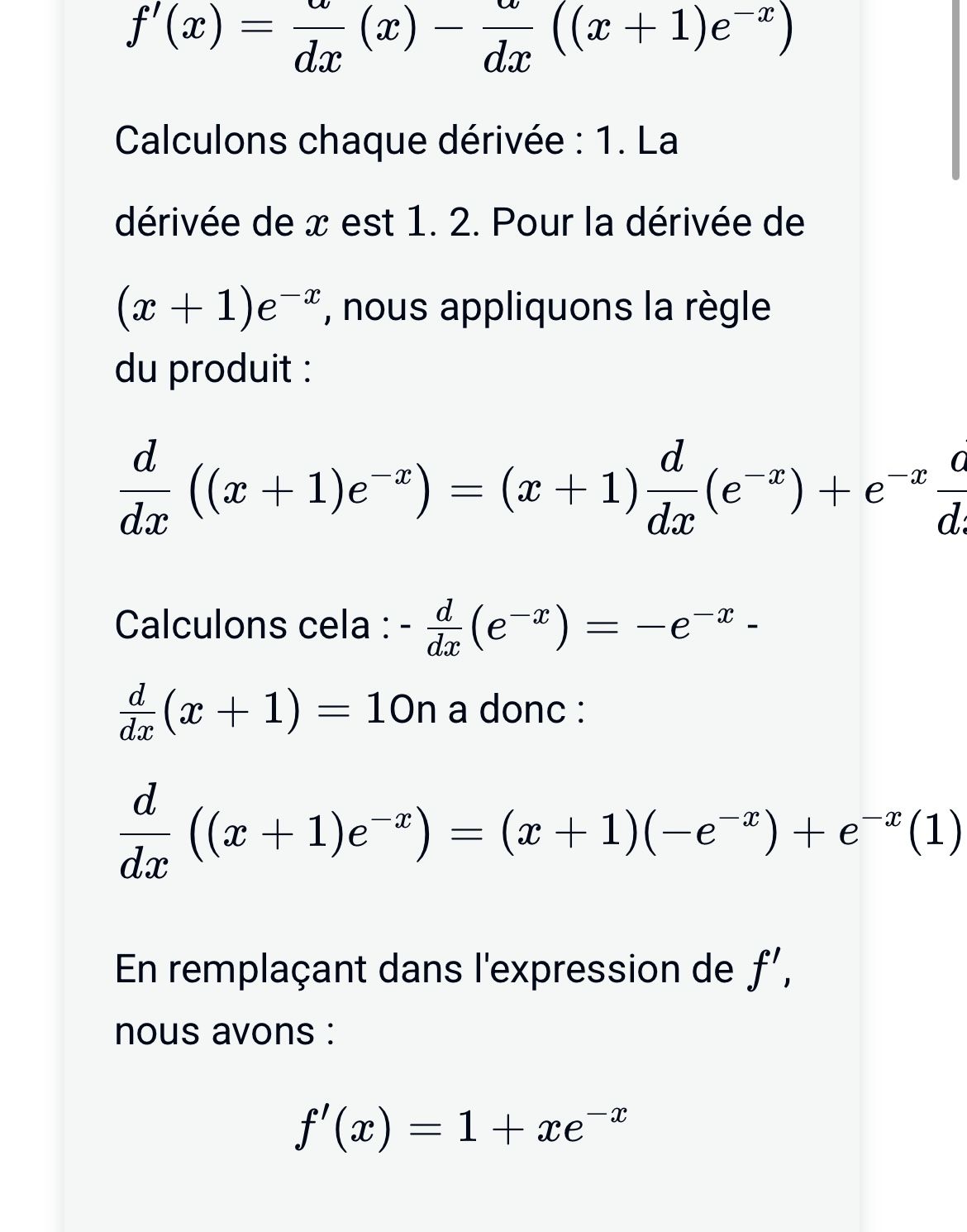
Le document est tronqué, il manque des éléments à droite.

La limite en $-\infty$ est fausse, il faut trouver $-\infty$ donc la partie 2 est à reprendre.

[hiba_mrcnn]

@Noemi

Je l’ai pas réussi

[hiba_mrcnn]

@Noemi

Je pourrais avoir une correction bien détaillé et préciser sur celle où c’est bon bon me le préciser entre parenthèses je vous remercie

[Noemi]

@hiba_mrcnn

Diminue la taille de ton document afin qu'on puisse lire la totalité.
Ou as-tu obtenu cette réponse ?

Pour la limite :
si $x$ tend vers $-\infty$, $e^{-x}$ tend vers $+\infty$ donc $x{e}^{-x}$ tend vers $-\infty$, soit $f^{\prime }(x)$ tend vers $-\infty$.

$f^{\prime }(0)=1$

Pour le tableau de variation de $f^{\prime }$, il faut calculer la dérivée seconde.
$f^{\prime \prime }(x)=e^{-x}-x{e}^{-x}=(1-x)e^{-x}$

Etudie le signe et fais le tableau de variations.

Je te laisse poursuivre. Indique tes calculs.

[hiba_mrcnn]

@Noemi

Oui c’est ça j’aimerai bien qu’on reprennes question par question s’il vous plaît

[hiba_mrcnn]

@Noemi

Commençons par ça

[Noemi]

@hiba_mrcnn

Tu veux commencer par quelle question ?

[hiba_mrcnn]

@Noemi

1

[Noemi]

@hiba_mrcnn

Pour la question 1.
Soit tu poses $u(x)=x$ et $v(x)=(x+1)e^{-x}$
puis tu calcules : $u^{\prime }(x)=1$ et $v^{\prime }(x)=e^{-x}-(x+1)e^{-x}=-x{e}^{-x}$
la dérivée : $f^{\prime }(x)=u^{\prime }(x)-v^{\prime }(x)=1+x{e}^{-x}$

Soit tu calcules directement la dérivée :
$f(x)=x-(x+1)e^{-x}$
$f^{\prime }(x)=1-[1\times e^{-x}+(x+1)\times (-e^{-x})]$
$f^{\prime }(x)=1-[e^{-x}-x{e}^{-x}-e^{-x}]$
soit
$f^{\prime }(x)=1+x{e}^{-x}$