Dm de maths sur les fonctions de référence

[zeus77390.]

Exercice 1 :
Considérons deux fonctions f et g définies par :
1
2
f( x)=3x²
–4x pour x∈ℝ et g( x)=
–
x
4−x
pour x≠0 et x≠4
1)a) Factoriser f( x)
b) Dresser le tableau de signes de f( x)
c) Résoudre f( x) > 0
2)a) Ecrire la fonction g( x) sous forme d’une seule fraction
b) Dresser le tableau de signes de g( x)
c) Résoudre g( x) ≤ 0
Exercice 2 :
≥ 3
Considérons l’inéquation 2
x+2

1. Déterminer une expression A( x) pour que l’in

[Noemi]

@zeus77390 Bonjour,

Rectifie l'écriture de $f(x)$ et $g(x)$
$g(x)=-\frac{?}{x(x-4)}$

Si $f(x)=3x^2-4x$

1. a) tu mets $x$ en facteur soit
   $f(x)=x(3x-4)$

je te laisse poursuivre, indique tes calculs.

[zeus77390.]

@Noemi bonjour ,je ne comprends pas le point d’interrogation à la première ligne

[zeus77390.]

@zeus77390 je n’ai plus de réponse de votre part ?

[Noemi]

@zeus77390

Le point d'interrogation correspond à la demande de rectification de l'écriture des fonctions.
Pour la fonction $g$, je ne vois pas le numérateur.
Est-ce $g(x)=\frac{-x}{4-x}$ ?
ou
$g(x)=-\frac{1}{x}+\frac{2}{4-x}$ ?

[Black-Jack]

@zeus77390 a dit dans Dm de maths sur les fonctions de référence :

@zeus77390 je n’ai plus de réponse de votre part ?

Ce que tu as écrit dans ta question initiale est incompréhensible.

voila ce que cela donne :

Exercice 1 :
Considérons deux fonctions f et g définies par :
1
2
f( x)=3x²
–4x pour x∈ℝ et g( x)=
–
x
4−x
pour x≠0 et x≠4

C'est complètement illisible.

Noemi a essayé de comprendre et a recopié les fonctions g(x) et f(x) qu'elle a cru voir ... mais elle n'en n'est pas sûre du tout.

Elle t'a donc demandé de réécrire correctement les fonctions f(x) et g(x) pour qu'elles soient compréhensibles ... et ceci avant de pouvoir t'aider.

[zeus77390.]

@Black-Jack ok d’accord je le réécris

[zeus77390.]

f( x)=3x²-4x pour x∈ℝ
g( x)=1/x -2/4-x
pour x≠0 et x≠4

1)a) Factoriser f( x)
b) Dresser le tableau de signes de f( x)
c) Résoudre f( x) > 0
2)a) Ecrire la fonction g( x) sous forme d’une seule fraction
b) Dresser le tableau de signes de g( x)
c) Résoudre g( x) ≤ 0

[Black-Jack]

Toujours pas clair pour g(x) ...

Est-ce que $g(x)=\frac{1}{x}-\frac{2}{4-x}$ ?

[Noemi]

@zeus77390

$g(x)$ doit être :
$g(x)=\frac{1}{x}-\frac{2}{4-x}$

Indique tes calculs et la question qui te pose problème.

[zeus77390.]

@Noemi oui c’est bien le calcul correct

[Noemi]

@zeus77390

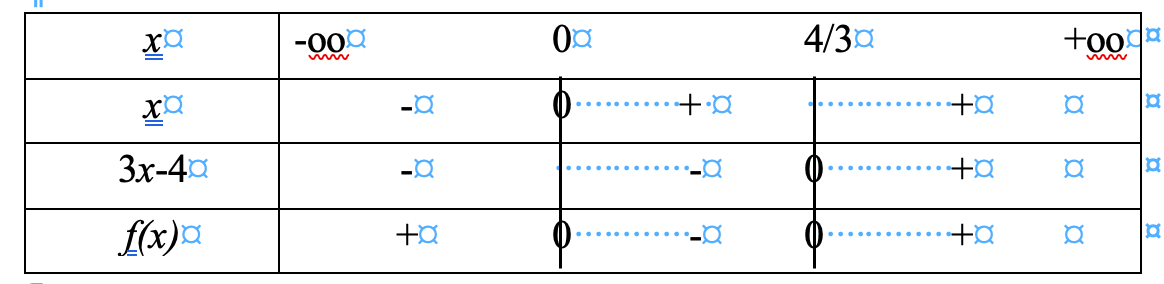
1.b) Commence par résoudre $f(x)=0$, puis dresse le tableau de signes :
$x$
$x$
$3x-4$
$f(x)$

c) Utilise les résultats de la questions b).

2.a) Réduis l'expression au même dénominateur :
$g(x)=\frac{1\times (4-x)-2\times x}{x(4-x)}=...$

[zeus77390.]

@Noemi oh la tu m’as perdu dès le début désolée

[Noemi]

@zeus77390

Tu ne sais pas résoudre $f(x)=0$, soit
$x(3x-4)=0$
Applique : Un produit de facteur est nul si et seulement si l'un de ses facteurs est nul.
Soit à résoudre :
$x=0$ et
$3x-4=0$

indique tes calculs.

[zeus77390.]

@Noemi c’est sa le calcul ? Car la je ne comprends vraiment rien

[Noemi]

@zeus77390

Tu postes en seconde, ce calcul est du programme de troisième, donc revois ton cours.
La résolution de l'équation $ax+b=0$ avec $a$ différent de 0 a pour solution :
$x=-\frac{b}{a}$.

[zeus77390.]

@Noemi c’est le problème c’est que je n’arrive pas à retenir

[Noemi]

@zeus77390

Ici je te demande d'appliquer.
$3x-4=0$ est bien de la forme $ax+b=0$
avec $a=...$ et $b=...$ donc $x=...$

[zeus77390.]

@Noemi a= 3 B=4 donc -1

[Noemi]

@zeus77390

Non
$a=3$ et $b=-4$ et $-\frac{b}{a}=....$

[zeus77390.]

@Noemi donc -4/3 c’est sa

[Noemi]

@zeus77390

Presque : $-\frac{b}{a}=-\frac{-4}{3}=\frac{4}{3}$

donc la première ligne du tableau de signes est :
$x$ $-\infty$ $0$ $\frac{4}{3}$ $+\infty$

[zeus77390.]

@Noemi je suis trop nul donc le calcul complet sa donne quoi vraiment

[Noemi]

@zeus77390

Il suffit d'écrire :
$3x-4=0$ donne $x=\frac{4}{3}$

[zeus77390.]

@Noemi donc la 1 a et b sont faites c’est ça

[zeus77390.]

@zeus77390 vous n’êtes plus là ?

[Noemi]

@zeus77390

La b) n'est pas terminé, tu dois faire le tableau de signes.

[zeus77390.]

@Noemi avec les signes que vous avez inscrit plus haut le tableau des signes c’est pareil je n’y comprends pas grand choses

[Noemi]

@zeus77390

Regarde le cours, comment est constitué un tableau de signes ?

[zeus77390.]

@Noemi oui c’est ce que j’ai fait

[Noemi]

@zeus77390

Regarde ce cours et suis les exemples. https://www.mathforu.com/seconde/factorisation-et-etude-de-signes-en-2nd/

Indique tes calculs.

[zeus77390.]

@Noemi comment sa

[zeus77390.]

@zeus77390 le calcul de 3x -4 = 0 ?

[Noemi]

@zeus77390

Pourquoi tu reviens sur le calcul de $3x-4=0$, tu n'as pas compris le raisonnement ?

[zeus77390.]

@Noemi non pas du tout je suis complètement perdu

[zeus77390.]

@zeus77390 j’ai tout relu et je me suis embrouillé les esprits

[Noemi]

@zeus77390

Donc reprends depuis le début. Ecris ce que tu as compris.

[zeus77390.]

@Noemi on a commencé par la question 1a où il fallait factoriser le calcul de f( x)=3x²
–4x pour x∈ℝ

[Noemi]

@zeus77390

Oui, As-tu compris la factorisation ?

[zeus77390.]

@Noemi bah pas trop j’avoue

[Noemi]

@zeus77390

Pour factoriser, il faut chercher le terme commun à $3x^2$ et $4x$
c'est deux termes comprennent la variable $x$, donc on peut mettre $x$ en facteur.
$3x^2-4x=3x\times x-4\times x=x(3x-4)$.

[zeus77390.]

@Noemi là on parle de f(x) c’est ça ?

[Noemi]

@zeus77390

oui c'est $f(x)$.

[zeus77390.]

@Noemi ok

[zeus77390.]

@zeus77390 ok mais je ne comprends pas

[zeus77390.]

@zeus77390 pourriez-vous me détailler le calcul s’il vous plaît

[Noemi]

@zeus77390

J'ai indiqué les calculs :
Pour factoriser, il faut chercher le terme commun à $3x^2$ et $4x$
c'est deux termes comprennent la variable $x$, donc on peut mettre $x$ en facteur.
$f(x)=3x^2-4x=3x\times x-4\times x=x(3x-4)$.

[zeus77390.]

@Noemi donc x= 3x-4

[zeus77390.]

@zeus77390 non à x = 3-4

[zeus77390.]

@zeus77390 ou X =4/3

[Noemi]

@zeus77390

Tu cherches quelle question ?

[zeus77390.]

@Noemi la suite du calcul que vous avez écris

[Noemi]

@zeus77390

Pour la question 1.a) le calcul est terminé

[zeus77390.]

@Noemi ah ok d’accord

[zeus77390.]

@zeus77390 maintenant c’est le tableau des signes

[Noemi]

@zeus77390

oui, passe à la question b).

[zeus77390.]

@Noemi les signes sont bien ceux que vous avez écrit plus haut

[zeus77390.]

@zeus77390 c’est bien ça ?

[Noemi]

@zeus77390

J'ai pas indiqué des signes.

[zeus77390.]

@Noemi ah bon je croyais avoir vu ça

[Noemi]

@zeus77390

Indique tes calculs.

[zeus77390.]

@Noemi
=3x2-4x par exemple

[zeus77390.]

@zeus77390 c’est bien ça

[Noemi]

@zeus77390

C'est pas un tableau de signes.

[zeus77390.]

@Noemi si c’est un tableau de signe

[zeus77390.]

C’est quoi comme tableau ?

[Noemi]

@zeus77390

Un tableau de signe comporte des signes + ou -
Une ligne du tableau pour exemple :
x - 0 +
Montre le résultat.

[zeus77390.]

@Noemi ah oui et là par exemple c’est quoi le résultat

[zeus77390.]

@zeus77390 je suis désolé mais j’ai du mal et je ne comprends rien

[Noemi]

@zeus77390

As-tu regardé le cours que je t'ai indiqué ?

[zeus77390.]

Oui j’ai regardé mais même comme ça

[Noemi]

@zeus77390

Que faut-il faire en premier ?

[zeus77390.]

@Noemi comment ça

[Noemi]

@zeus77390

Pour faire un tableau de signe d'une fonction, quel calcul est à faire au début ?
Etape 1 du cours ?

[zeus77390.]

@Noemi je sais pas

[Noemi]

@zeus77390

Regarde le cours.

[zeus77390.]

@Noemi on résout chaque équation

[Noemi]

@zeus77390

Cherche les valeurs qui annule la fonction.

[zeus77390.]

Je sais pas

[Noemi]

@zeus77390

Tu résous $f(x)=0$. j'ai déjà indiquer les calculs.

Regarde cette vidéo : https://www.youtube.com/watch?v=50CByVTP4ig

[zeus77390.]

@Noemi je comprends pas

[Noemi]

@zeus77390

Indique ce que tu ne comprends pas.

[zeus77390.]

@Noemi tout c’est sa le pire

[Noemi]

@zeus77390

Tu n'as jamais fait de tableau de signes ?

[zeus77390.]

@Noemi si mais je ne comprends pas je trouve sa trop dur

[Noemi]

@zeus77390

Pourtant, il suffit d'appliquer le cours.

[zeus77390.]

@Noemi même avec le cours je suis complètement paumé

[Noemi]

@zeus77390

Difficile de t'aider si tu n'indiques pas ce que tu ne comprends pas.

[zeus77390.]

@Noemi la façon de mettre les signes et pourquoi

[Noemi]

@zeus77390

Pour les signes, tu appliques la règle du cours.
pour $ax+b$ c'est du signe de $a$ à droite de la valeur qui annule $ax+b$ et du signe de $-a$ à gauche.

Exemple

1. $3x-2$, s'annule si $x=\frac{2}{3}$, donc on écrira pour le signe de
   $3x-2$ ; $-0+$

2. $-x+5$, s'annule si $x=5$, donc on écrira pour le signe de
   $-x+5$ : $+0-$.

[zeus77390.]

@Noemi oui mais c’est très dur

[Noemi]

@zeus77390

Il faut comprendre et apprendre.

[zeus77390.]

@Noemi je n’arrête pas je peux vous assurer je veux réussir mes études la question c maintenant ?

[Noemi]

@zeus77390

Pour la question c), il faut écrire les intervalles pour lesquels la fonction est positive. Soit regarder dans le tableau la ou se trouve le signe $+$ et écrire les intervalles correspondant à la variable $x$.

[zeus77390.]

@Noemi est ce que c’est sa ? x E] - ♾️0[U]4/3, +∞0[.

[Noemi]

@zeus77390

C'est juste. Un 0 en trop à la fin.

Passe à la question 2.
$g(x)=\frac{1}{x}-\frac{2}{4-x}$
Pour réduire au même dénominateur :
$g(x)=\frac{1\times (4-x)-2\times x}{x(4-x)}$

Développe et simplifie le numérateur.

[zeus77390.]

@Noemi
g(x)=1/4-x -1/2 = 2-(4-x)/2(4-x) = 2-4+x/2(4-x) = x-2/ 2(4-x) c’est sa ?

[Noemi]

@zeus77390

Tu as précisé que la bonne relation pour $g(x)$ était :
$g(x)=\frac{1}{x}-\frac{2}{4-x}$ (1)
et
tu écris (sauf erreur) que
$g(x)=\frac{1}{4-x}-\frac{1}{2}$ (2)

Pour l'expression (1) :
$g(x)=\frac{1\times (4-x)-2\times x}{x(4-x)}=\frac{4-x-2x}{x(4-x)}=....$

Pour l'expression (2)
$g(x)=\frac{1\times 2-1\times (4-x)}{2(4-x)}=\frac{2-4+x}{2(4-x)}=\frac{x-2}{2(4-x)}$ qui correspond à ton résultat.

[zeus77390.]

@Noemi ce n’est pas bon ce que j’ai fait ?

[Noemi]

@zeus77390

Ton calcul est correct si la fonction $g$ est :
$g(x)=\frac{1}{4-x}-\frac{1}{2}$

Ce n'est pas cette fonction que tu avais validée dans un post précédent.

[zeus77390.]

@Noemi ah oui mince je n’avais pas fait attention il étais tard donc c’est ce que tu as écris la bonne réponse

[Noemi]

@zeus77390

Si la bonne relation pour $g(x)$ est :
$g(x)=\frac{1}{x}-\frac{2}{4-x}$

alors :
$g(x)=\frac{1\times (4-x)-2\times x}{x(4-x)}=\frac{4-x-2x}{x(4-x)}=\frac{4-3x}{x(4-x)}$

[zeus77390.]

@Noemi oui mais là ce n’est pas le cas c’est ta réponse qui est Bonne c’est sa

[Noemi]

@zeus77390

Si $g(x)=\frac{1}{x}-\frac{2}{4-x}$, mon précédent post donne la réponse.

[zeus77390.]

@Noemi
Si je met au même dénominateur
4-x/x(4-x) - 2x/x(4-x) = 4-x-2x/x(4-x) = 4-3x/ x(4-x)

[Noemi]

@zeus77390

C'est juste,
pour une lecture plus correcte, il faudrait mettre des parenthèses pour bien identifier numérateur et dénominateur.
soit
(4-x)/(x(4-x)) - (2x)/(x(4-x)) = ...

b) Dresse le tableau de signes.

[zeus77390.]

@Noemi je suis trop contente j’ai réussi Les racines sont 4 - 3x = 0 → x = 3/
x = 0 et 4 - x = 0 → x = 4.

• On a donc trois valeurs à prendre en compte 0, 4/3 , 4

[Noemi]

@zeus77390

Oui c'est juste.
Attention, tu as écris à la fin de la première ligne $x=3/$ . au lieu de $x=4/3$

Fais le tableau de signes.

[zeus77390.]

@Noemi ah oui une erreur de frappe désolé
Le tableau c’est | x| -♾️| 0 | | 4/3 | | 4 | | +♾️|

[Noemi]

@zeus77390

Oui pour la première ligne pas utile de mettre 2 traits verticaux.

[zeus77390.]

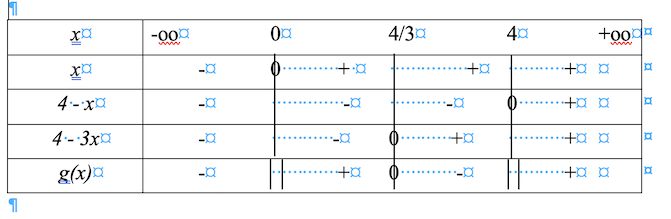
|4-3x| + | + | + | 0 |- | - | - |
| X | - | 0 | + | + | +| +| + |
| 4-x | + | + | + | + | +| + | 0
| g(x) | -| + | 0 | - | + | - | |
Tu en penses quoi ?

[Noemi]

@zeus77390

Rectifie, tu as 4 intervalles, donc que 4 signes à indiquer pour chaque intervalles.

[zeus77390.]

@zeus77390 a dit dans Dm de maths sur les fonctions de référence :

|4-3x| + | + | + | 0 |
| X | - | 0 | + | + |
| 4-x | + | + | + | + |
| g(x) | -| + | 0 | - |
comme ça ?

[zeus77390.]

@zeus77390 vous avez fait un tableau plus haut si j’ai j’ai bon j’aimerais voir le votre pour cet question

[Noemi]

@zeus77390

Le 0 n'est pas un signe. Chaque ligne va comporter au mois 1 + et un -.

[zeus77390.]

@zeus77390 a dit dans Dm de maths sur les fonctions de référence :

@zeus77390 a dit dans Dm de maths sur les fonctions de référence :

|4-3x| + | + | + | 0 | -|
| X | - | 0 | + | + | +|
| 4-x | + | + | + | + |0 |
| g(x) | -| + | 0 | - | +|
la c’est bon cet fois

[Noemi]

@zeus77390

La troisième ligne est fausse.

Tu dois trouver :

[zeus77390.]

@zeus77390 a dit dans Dm de maths sur les fonctions de référence :

@zeus77390 a dit dans Dm de maths sur les fonctions de référence :

@zeus77390 a dit dans Dm de maths sur les fonctions de référence :

|4-3x| + | + | + | 0 | -|
| X | - | 0 | + | + | +|
| 4-x | + | + | + |0 | -|
| g(x) | -| + | 0 | - | +|
et la ?

[Noemi]

@zeus77390

J'ai indiqué la réponse. Compare avec ton résultat, il manque les valeurs interdites (2 traits verticaux).

Passe à la question c). Tu analyses le tableau.

Pour l'exercice 2, il faut ouvrir un autre sujet et bien écrire l'énoncé.

[zeus77390.]

@Noemi
D'après le tableau de signes, g (x) ≤ 0
lorsque x E] - ♾️,0[U[ 4/3 ,4 [ c’est le bon résultat ?

[Noemi]

@zeus77390

C'est juste. Bon travail.

[zeus77390.]

@Noemi merci c’est cool

[Noemi]

@zeus77390

Tu peux chercher l'exercice 2 c'est le même raisonnement.

[zeus77390.]

@Noemi je veux juste être sure de ne pas me tromper