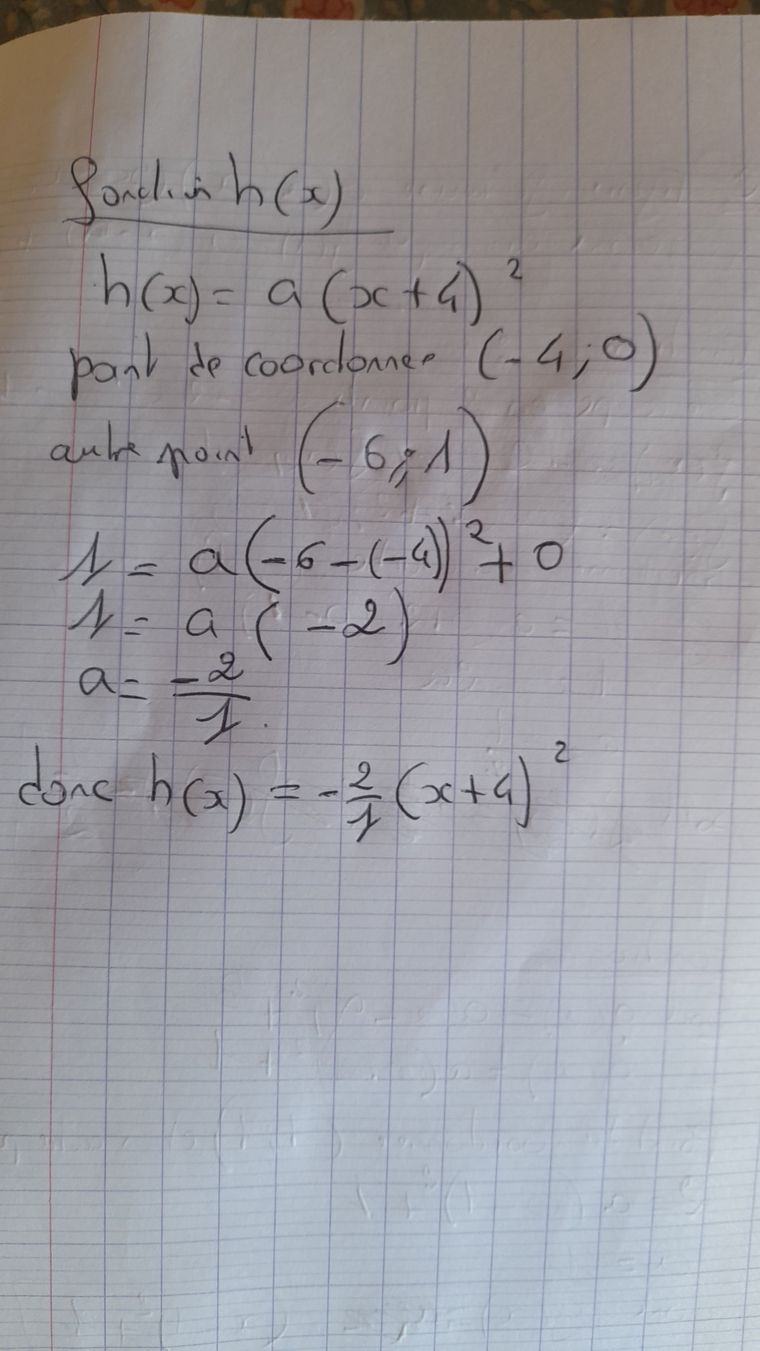Fonctions polynomiales

[m12]

Dernier exercice
J arrive pas à résoudre

F g et h sont 3 fonctions de degré 2

1. lorsqu'elle existe donner la forme factoriser de chaque fonction

2. donner la forme canonique de g et h
   

[m12]

@m12 a dit dans Fonctions polynomiales :

Dernier exercice
J arrive pas à résoudre

F g et h sont 3 fonctions de degré 2

1. lorsqu'elle existe donner la forme factoriser de chaque fonction

2. donner la forme canonique de g et h
   

Pour moi lla courbe g coupe pas axe des abscisses donc pas de forme factoriser

[Noemi]

@m12 Bonjour,

Commence par chercher pour quelle(s) valeur(s) de $x$ la fonction s'annule.
Pour $f$, $x_1=...$ et $x_2=....$
donc ....

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12 Bonjour,

Commence par chercher pour quelle(s) valeur(s) de $x$ la fonction s'annule.
Pour $f$, $x_1=...$ et $x_2=....$
donc ....

Je commence par la courbe f elle coupe x en 2 points
X=-2 r x=1
Donc formule factoriser a(x-x1)(x-x2)
F(x)) = a(x+2)(x-2)

[Noemi]

@m12

Comme $x_2=1$ $f(x)=a(x+2)(x-1)$
pour déterminer la valeur de $a$, utilise les coordonnées du point de la courbe qui coupe l'axe des ordonnées.

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Comme $x_2=1$ $f(x)=a(x+2)(x-1)$
pour déterminer la valeur de $a$, utilise les coordonnées du point de la courbe qui coupe l'axe des ordonnées.

X=-2 et 2
Y= 1
Cesr cela ?

[Noemi]

@m12

Non, les coordonnées du point de la courbe qui coupe l'axe des ordonnées sont :
$(0;1)$ que tu remplaces dans $f(x)=a(x+2)(x-1)$ et tu résous l'équation pour déterminer la valeur de $a$.

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Non, les coordonnées du point de la courbe qui coupe l'axe des ordonnées sont :
$(0;1)$ que tu remplaces dans $f(x)=a(x+2)(x-1)$ et tu résous l'équation pour déterminer la valeur de $a$.

F(x) = (x-(-2))(x-1)

[Noemi]

@m12

$f(x)=a(x+2)(x-1)$ tu dois trouver la valeur de $a$.
le point de coordonnées $(0;1)$ appartient à la courbe, donc tu remplaces $x$par $0$ et $y$ par $1$ pour déterminer la valeur de $a$.
Soit à résoudre l'équation :
$1=a(0+2)(0-1)$
en simplifiant :
$1=-2a$, soit
$a=...$
que tu remplaces dans l'expression de $f(x)$.
Soit $f(x)=....$

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

$f(x)=a(x+2)(x-1)$ tu dois trouver la valeur de $a$.
le point de coordonnées $(0;1)$ appartient à la courbe, donc tu remplaces $x$par $0$ et $y$ par $1$ pour déterminer la valeur de $a$.
Soit à résoudre l'équation :
$1=a(0+2)(0-1)$
en simplifiant :
$1=-2a$, soit
$a=...$
que tu remplaces dans l'expression de $f(x)$.
Soit $f(x)=....$

OK-1/2

[Noemi]

@m12

Oui,

Pour les deux autres fonctions, il faut utiliser l'écriture de la fonction sous forme canonique, soit $g(x)=a(x-\alpha {)}^2+\beta$. le sommet de la courbe a pour coordonnées $(\alpha ;\beta )$.
As-tu cette relation dans ton cours ?

Si oui, commence par déterminer les coordonnées du minimum de la courbe $g$.

[m12]

@m12 a dit dans Fonctions polynomiales :

@Noemi a dit dans Fonctions polynomiales :

@m12

$f(x)=a(x+2)(x-1)$ tu dois trouver la valeur de $a$.
le point de coordonnées $(0;1)$ appartient à la courbe, donc tu remplaces $x$par $0$ et $y$ par $1$ pour déterminer la valeur de $a$.
Soit à résoudre l'équation :
$1=a(0+2)(0-1)$
en simplifiant :
$1=-2a$, soit
$a=...$
que tu remplaces dans l'expression de $f(x)$.
Soit $f(x)=....$

OK-1/2

-1/-2

[Noemi]

@m12

C'est quoi ce -1/-2 ?

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Oui,

Pour les deux autres fonctions, il faut utiliser l'écriture de la fonction sous forme canonique, soit $g(x)=a(x-\alpha {)}^2+\beta$. le sommet de la courbe a pour coordonnées $(\alpha ;\beta )$.
As-tu cette relation dans ton cours ?

Si oui, commence par déterminer les coordonnées du minimum de la courbe $g$.

Non j ai pas encore fait
Mais dans la question 2 il demande juste forme factoriser donc
Pour g comme sa coupe pas x il y a pzs de forme factoriser
Et pour h
X=-4
H(x)= a((x+4)carre

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

C'est quoi ce -1/-2 ?

Je sais pas si cet -1/2 ou -1/-2

[Noemi]

@m12

C'est $-1/2$ pour la valeur de $a$ de la fonction $f$.

L'énoncé demande la forme canonique pour $g$ et $h$.
Donc
$g(x)=a(x-1{)}^2+1$ et
$h(x)=a(x+4{)}^2$

Il reste à déterminer la valeur de $a$ à partir d'un point de la courbe.

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

C'est $-1/2$ pour la valeur de $a$ de la fonction $f$.

L'énoncé demande la forme canonique pour $g$ et $h$.
Donc
$g(x)=a(x-1{)}^2+1$ et
$h(x)=a(x+4{)}^2$

Il reste à déterminer la valeur de $a$ à partir d'un point de la courbe.

Donc la il y a déjà forme canonique ?
Point de la courbe h = -4
Point courbe g =1

Mais comme g ce coupe pas en x?

[Noemi]

@m12

Attention les coordonnées d'un point c'est (abscisse ; ordonné).
Pour la courbe $g$ : $(1;1)$
Pour la courbe $h$ : $(-4;0)$

Pour déterminer la valeur de $a$, tu choisis un autre point de la courbe.
Par exemple pour $g$, le point de coordonnée $(0;2)$
soit à résoudre : $2=a(0-1{)}^2+1$
...

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Attention les coordonnées d'un point c'est (abscisse ; ordonné).
Pour la courbe $g$ : $(1;1)$
Pour la courbe $h$ : $(-4;0)$

Pour déterminer la valeur de $a$, tu choisis un autre point de la courbe.
Par exemple pour $g$, le point de coordonnée $(0;2)$
soit à résoudre : $2=a(0-1{)}^2+1$
...
Je suis perdu

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Attention les coordonnées d'un point c'est (abscisse ; ordonné).
Pour la courbe $g$ : $(1;1)$
Pour la courbe $h$ : $(-4;0)$

Pour déterminer la valeur de $a$, tu choisis un autre point de la courbe.
Par exemple pour $g$, le point de coordonnée $(0;2)$
soit à résoudre : $2=a(0-1{)}^2+1$
...

2=a×00
A= -2

[Noemi]

@m12

Pour la fonction $g$.
Tu utilises l'écriture de la fonction sous forme canonique, soit $g(x)=a(x-\alpha {)}^2+\beta$. le sommet de la courbe a pour coordonnées $(\alpha ;\beta )$.
Pour $g$ le sommet a pour coordonnées $(1;1)$
Soit
$g(x)=a(x-1{)}^2+1$

Pour déterminer la valeur de $a$, tu choisis un point de la courbe $g$
Soit par exemple : $(0;2)$
donc
$2=a(0-1{)}^2+1$
équation à résoudre.

[Noemi]

@m12

Non,
C'est $2=a+1$ soit $a=....$

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Pour la fonction $g$.
Tu utilises l'écriture de la fonction sous forme canonique, soit $g(x)=a(x-\alpha {)}^2+\beta$. le sommet de la courbe a pour coordonnées $(\alpha ;\beta )$.
Pour $g$ le sommet a pour coordonnées $(1;1)$
Soit
$g(x)=a(x-1{)}^2+1$

Pour déterminer la valeur de $a$, tu choisis un point de la courbe $g$
Soit par exemple : $(0;2)$
donc
$2=a(0-1{)}^2+1$
équation à résoudre.

a=1

[Noemi]

@m12

Oui,
Donc $g(x)=(x-1{)}^2+1$
Tu appliques la même démarche pour la fonction $h$.
$h(x)=a(x+4{)}^2$

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Oui,
Donc $g(x)=(x-1{)}^2+1$
Tu appliques la même démarche pour la fonction $h$.
$h(x)=a(x+4{)}^2$

OK je fzis une pause he reprendrais plus tard

[Noemi]

@m12

Ok.
A+

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Ok.
A+

@Noemi a dit :

@m12

Ok.
A+

[Noemi]

@m12

Tu as oublié d'élever au carré.
$1=a(-6+4{)}^2$
$1=a(-2{)}^2$
$1=4a$
$a=\frac{1}{4}$
$h(x)=....$

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Tu as oublié d'élever au carré.
$1=a(-6+4{)}^2$
$1=a(-2{)}^2$
$1=4a$
$a=\frac{1}{4}$
$h(x)=....$

Ah oui mince
H(x) = 1/4(x+4) au carre

[Noemi]

@m12

C'est correct.

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

C'est correct.

OK merci
C était difficile

Du coup l exo est fini
Puisque on a la forme factoriser de f et les formes canonisue de g et h?

[Noemi]

@m12

Oui, l'exercice est terminé.

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Oui, l'exercice est terminé.

Ouf il m à fait suer lol
Merci à vous de votre aide car sinon c'est de la torture

[Noemi]

@m12

J'espère que tu as tout compris.

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

J'espère que tu as tout compris.

Oui sa va
Je vais revoir tout cela à tête reposez
En résumé faut savoir ses formule factoriser er canonique par coeur

[Noemi]

@m12

Ok, N'hésite pas à poser des questions si tu as un doute sur un calcul.

[m12]

@Noemi a dit dans Fonctions polynomiales :

@m12

Ok, N'hésite pas à poser des questions si tu as un doute sur un calcul.

Oui merci à vous