Fonction derivable

Voila, encore un autre petit exerciceincompris de ma part.

Soit f la fonction definie par :

f(x)= (x-1)² / (x+1)

et Cf sa courbe representative dans le plan rapporte a un repere orthonormal ou l'unite graphique est le cm.

1°Montrer que f est derivable sur son ensemble de definition Df et calculer f '(x).

2°
a. Etudier le signe de f '(x) sur Df.
b. En deduire les variations de f.
c. Dresser le tableau de variation de f.

3°Montrer qu'il existe trois reels a, b et c tels que pour tout x de Df :
f(x) = ax + b + c/(x+1)

4°Soit D la droite d'equation y = ax + b ou a et b sont les reels precedents.
a. Etablir la courbe Cf est au-dessus de la droite D quand x appartient a l'intervalle I.
b. Pour un x de I, on note d(x) la distance entre les points de D et de Cf de meme abscisse x. Montrer que cette distance diminue lorsque x augmente.
c. Si l'on utilise de 0.5mm pour tracer la courbe, a partir de quelles valeurs de x ne fera-t-on plus la difference entre D et Cf ?

Voila, je sais ca fait beaucoup mais je demande pas les reponses, mais des aides. ^^

Sinon, la 1°, elle est facile, je vais vous montrer ma reponse :

Df = $mathbb{R}$ / {-1}

La fonction f est le quotient des fonctions u et v tel que :
u(x) = (x - 1)² et v(x) = x + 1

Pour la fonction u, il faut differencier les deux composé de la fonction en deux fonctions g et h tels que :
g(x) = x² et g'(x) = 2x
h(x) = x-1 et h'(x) = 1

Et u(x) = goh(x) donc u'(x) = g'(h(x)) * h'(x) = 2(x-1)+1 = 2x - 1
Et v'(x) = 1

f '(x) = (u/v)'(x) = (u'(x)v(x) - u(x)v'(x)) / (v(x))²
f '(x) = [ (2x-1)(x+1) - (x-1)² * 1 ] / (x+1)²
Apres developpement :
f '(x) = (x²+3x -2) / (x²+2x+1)

Le trinome du second degre au denominateur :
delta = b² - 4ac = 2² - 411 =0
Solution double :
x = -b / 2a = -2 / 2*1 = -1

Donc Df' = Df = $mathbb{R}$ / {-1}

Voila, dites moi si j'ai deja fait une erreur. Merci de vos futurs coups de pouce.

donc pour la 1° ce que tu as fait est bien, sauf une erreur de calcul ici :
g'(h(x)) * h'(x) = 2(x-1)+1 = 2x - 1 (le * s'est transformé en +)
Je te laisse alors refaire tes calculs et faire le tableau de variation.

Merci raycage, grace a toi j'ai rectifier mon erreur :

f '(x) = [(2x-1)(x+1) - (x-1)²*x] / (x+1)²
f '(x) = (x²+ 2x-3) / (x+1)²

(x+1) est forcement positif

x²+2 x-3 est un trinome du second degre
delta= 2²+4*3 = 16 = 4²
Deux solutions disctinctes :
x1= (-2-4) / 2 = -6 / 2 = -3 et x2= (-2+4) / 2 = 2/2 = 1
Comme a>0, le trinome est positif a l'exterieur des racines

x____________-oo_____-3_____-1_____1_____+oo
x²+ 2x-3__________+0--0+
(x+1)²____________++0++____
f'(x)____+0--0+

Voila, si vous arrivez vraiment pas a lire, je ferais un tableau paint puis un scan de l'ecran.

Apres, je sais pas trop comment on deduit les variations de f a partir de ce tableau. Enfin, je peut le faire, mais uniquement parce que j'ai tracé la courbe sur ma calculette. XD

A+, merci de votre aide.

On a grâce au tableau de signe, le signe de f'(x). Eh bien, si f'(x) est positif, f est croissante, s'il est négatif, f est décroissante. Voilà !

Je comprend pas trop :
Sur l'intervalle [-1 ; 1], f(x) est croissante et pourtant f '(x) est negatif.

Citation
f '(x) = [(2x-1)(x+1) - (x-1)²*x] / (x+1)²
Encore des erreurs dans le calcul de la dérivée : d'où vient le 2x-1 dans le premier terme, et pourquoi y a-t-il un x dans le deuxième terme ?

Faute de frappe, c'etait (x-1)²*1, mais t'inquiete j'ai fait avec le 1 sur mon brouillon. Mais sinon, le resultat final de f '(x) est faux ?

Et pour la question que je viens de poser, as-tu la reponse ?

Merci de votre soutien mental (demoralisé) et physique (souffrance)

Sinon, pour mon tableau de variation, j'obtient :

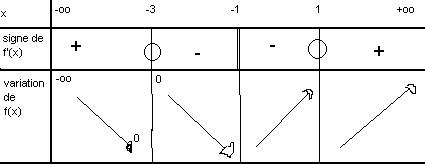
oui le résultat final est faux, car ce n'est pas 2x-1 dans le premier terme de ta dérivée, la dérivée de (x-1)² est ?

Ma stupidité m'enerve. Mais la encore, c'est une faute de frappe. Sur mon brouillon j'ai bien mis 2x - 2.
Et donc, normalement, je devrais avoir le bon resultat.

Ah non ! C'est pas une faute de frappe, c'est que pour gagner du temps, j'avais copier coller cette egalité que j'avais deja note avant que tu me dise que je mettais trompe. Mais le resultat final est bon, du moins je l'espere.

oui donc c'est bon, pourquoi veux-tu que f soit croissante sur [-1,1] ?
Et pourquoi l'as-tu faite décroissante sur [-∞,-3] ?

Mince, j'ai confondue la derivé avec la fonction.

Non, donc en faites sa donne :
Croissante sur ]-oo ; -3] U [1 ; +oo[
Decroissante sur [-3 ; -1[ u ]-1 ; 1]

Et ca me donne ca :

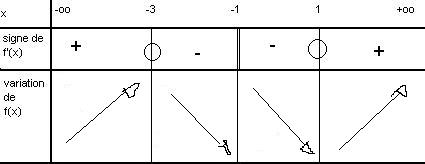
Sinon, la question 3°, je n'y comprend rien de rien a comment je suis censé m'y prendre :
3°Montrer qu'il existe trois reels a, b et c tels que pour tout x de Df :
f(x) = ax + b + c/(x+1)

Merci encore et toujours de ton aide.

f(x) = ax + b + c/(x+1), tu mets toute cette expression sur le même dénominateur et tu compares ensuite à l'expression de f pour voir s'il n'y aurait pas des nombres a b et c qui feraient que les deux soient égales.

J'ai fait ce que tu m'as dit, a la fin j'arrive :

(ax² + (a+b)x + b + c) / x+1
(x-1)² = x² - 2x + 1
J'utilise la methode par identification et ca me donne :

a = 1
a+b = -2 <=> b = -3
b+c = 1 <=> c = 4

Voila, et pour la 4°a. j'imagine qu'il faut faire : y - f(x) = r
Si r>0 , alors la droite D est au dessus de Cf
Si r<0 , alors la droite D est au dessous de Cf
s r=0 , alors la droite D et la courbe Cf se rapproche

oui c'est bon, pour la 4 la méthode est bonne aussi.

Ca y est, j'en suis a la 4°b :
b. Pour un x de I, on note d(x) la distance entre les points de D et de Cf de meme abscisse x. Montrer que cette distance diminue lorsque x augmente.

d(x) = 4 / (x+1)
Pour prouver que d(x) diminie quand x augmente, faut utiliser la derivée de d(x) ?

EDIT : Ah oui ! C'est ca, si d'(x) positif, alors d(x) est croissant.

Comme je fait souvent des erreurs betes dans mes calculs (voir plus haut ^^), j'aimerais qua vous me confirmiez mon calcul :
f(x') = (x'-1)² / (x'+1)
avec x' = 2a - x et a = -1
Donc x' = -2 - x
Le but est de supprimez les x' par des x et de simplifiez.
Mon resultat est :
f(x') = (x'-1)² / (x'+1) = (x² + 6x +9) / (-x - 1)

Et une petite question : comment prouve-t-on qu'un ensemble de definition Df est centré en a ?

Petit up avec une news :

Comment mettre au meme denominateur ca :
[ (x² - 2x + 1) / (x + 1) ] + [ (x² + 6x +9) / (-x - 1) ]

Je sais, c'est une regle de base, mais devant le fait accomplie, des fois j'oublie les bases.

Et sinon, pour mon post precedent, pourriez vous me repondre.

Encore et toujours, merci !

Pour l'avant-dernier message je ne comprends pas ce que tu essaies de calculer mais le calcul semble bon.
Pour ton dernier message, tu écris -x-1=-(x+1) et tu t'aperçis qu'en fait les deux fractions sont déjà sur le même dénominateur au signe près, tu n'as donc plus qu'à ajouter les numérateurs.