Un rectangle inscrit dans un triangle
-
Llolival dernière édition par
Bonjour bonjour !!!
Petit problème de maths :
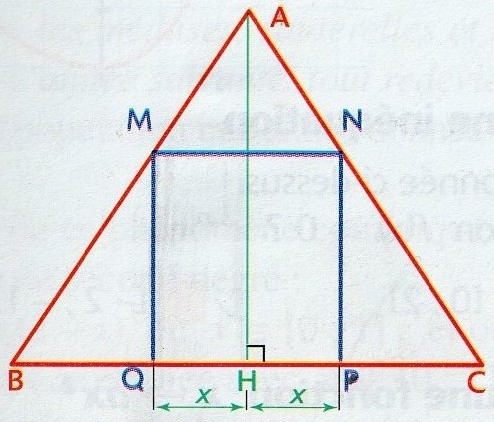
ABC est un triangle isocèle en A avec BC=12
H est ke pied de la hauteur issue de A et AH=9
P et Q sont deux points de [BC] symétriques par rapport à H, on note HP=HQ=xOn se propose de déterminer les dimensions du rectangle MNPQ d'aire maximale inscrit dans ce triangle.
1)a. Démontrer que MQ=18-3x/2
Sur cette première question je me demande dans quel triangle nous devons travailler (BMQ ? BMC ?), est-il necéssaire de connaître AB et AC ? ( Qui sont facile à trouver
 )
)Merci de votre aide

-
JJeet-chris dernière édition par
Salut.
Tu dois pouvoir utiliser le théorème de Thalès dans BMQ et BHA une fois que tu auras justifié que (MQ) et (HA) sont parallèles.
@+
-
Llolival dernière édition par
Merci

Mais pour prouver que MQ et HA sont parallèle je dois prouver que BQM est rectangle en Q ?
Ensuite je dis que si deux droite sont perpendiculaires à une même droite alors elles sont parallèles ?
-
Zauctore dernière édition par

salut
du fait du rectangle... tu as clairement (QM) perpendiculaire à (HQ).
-
Llolival dernière édition par
Ok !
Merci beaucoup !Ensuite je trouve que:
A(x)=-3[(x-3)²-9] définie sur R
Sur [0;3] elle est croissante et sur [3;6] elle est décroissanteC'est tout ce que j'ai prouvé mais là question 3)a) je n'y arrive pas :
Montrer que la fonction A admet un maximum, quelle est sa valeur ??
Merci pour votre aide

-
Zauctore dernière édition par

re.
fonction croissante puis décroissante : parabole tournée vers le bas : le sommet te donne le maximum cherché.
-
Llolival dernière édition par
Huuuum, quand x=3 alors ?
donc les dimensions du rectangle d'aire maximale est :
A(x)=-3[(x-3)²-9]
A(3)=-3[(3-3)²-9]
A=27Est-ce bon ?!!!
Merci beaucoup en tout cas !
-
Ssea-hawk dernière édition par
Comment avez-vous réussis à trouver MQ= 18-3x/2 ?
Je suis dessus depuis tout à l'heure! et ca me paraît tellement bête pourtant... :frowning2:
-
Tu as appliqué les conseils donnés par Zauctore et jeet-chris plus haut ? (Utiliser le théorème de Thalès)
-
Ssea-hawk dernière édition par
Autant pour moi! Je me suis trompée dans une valeur! Tout s'éclaire. Merci en tous cas
