Je ne dis pas que je ne sais pas ce que sont deux droites orthogonales. Simplement que cela ne figure pas dans mon cours, donc j'imagine qu'il ne faut pas l'utiliser

On n'a pas encore vu cette notion de perpendiculaire / orthogonale. On a juste vu que deux droites peuvent être soit coplanaires (parallèles strictes, confondus, sécantes) ou non-coplanaires

(AD) et (GM) ne sont pas dans le même plan. (AD) appartient à (ADH) alors que (GM) appartient à (GMC). Donc non (AD) et (GM) non coplanaires

Merci. Mais, malheureusement, je n'ai pas encore vu les coordonnées dans l'espace.

"complanaires" est une erreur de frappe. Je voulais dire "coplanaires".

Bonjour,
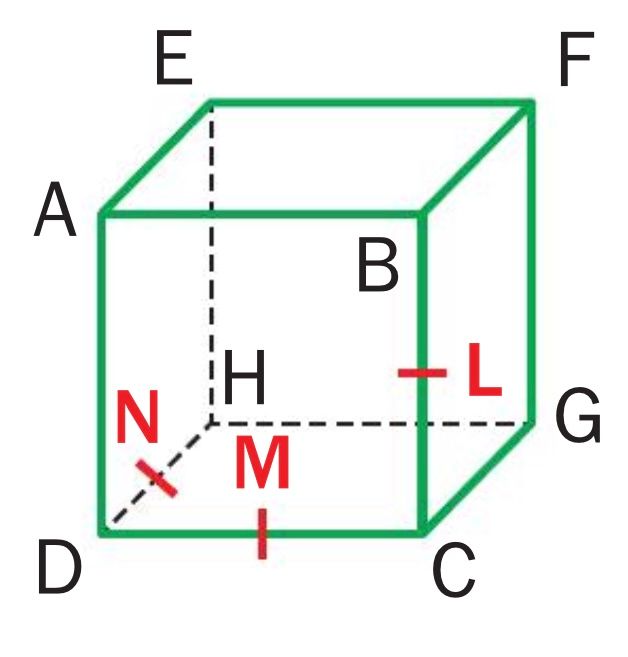
ABCDEFGH est un cube. L,M et N sont les milieux des segments [BC] [DC] et [DH]. Détemriner, en justifiant, les positions relatives des droites et plans suivants.

J'ai réussi à montrer (ML) et (HF) sont parallèles avec la relation de Chasles :
ML = MC + CL
<=> ML = 1/2DC+1/2CB
<=> ML = 1/2DB
<=> ML = 1/2 HF
D'où ML et HF sont colinéaires. Donc (ML)//(HF) et (ML) et (HF) coplanaires.

J'ai aussi réussi à montrer qye (HM) et (CG) sont complanaires sécantes :
(HM) C (DCG) et (CG) C (DCG).
Donc (HM) et (CG) sont complanaires.
(HM) et (DH) sont sécantes en H et (CG) // (DH). Or si deux droites sont parallèles, alors tout droite sécante à l'une est sécante à l'autre. Donc (HM) et (CG) sont sécantes.

Mais je bloque pour (AD) et (GM). Merci pour votre aide![text alternatif]

Oui, j'avais juste oublié les parenthèses ! Désolée pour le dérangement

Bonjour,
Je me sens un peu bête, mais pour l'exercice suivant, je n'arrive pas à trouver la bonne égalité à montrer dans l'hérédité :

Démontrer par récurrence, que pour n appartenant à N* : 1²+2²+...+n² = ((n(n+1)(2n+1))/6.

J'ai bien sûr fait l'initialisation pour n = 1.

Mais je bloque pour l'égalité à montrer dans l'hérédité. Je trouve : 1²+2²+...+(n+1)² = ((n+1)(n+2)(2n+2))/6 à la place de 1²+2²+...+(n+1)² = ((n+1)(n+2)(2n+3))/6.

Merci

Merci, je vais regarder la vidéo

Bonsoir,
J'ai juste besoin d'aide pour la conlusion de l'exercice suivant :
LENA est un tétraèdre.
R, S et T sont les points définis par :
LR = 1/3LE ; LS=1/3LN et LT=1/3LA.
Démontrer que les plans (RST) ET (ENA) sont parallèles.

J'ai montré que RS et EN sont colinéaires et RT et EA sont colinéaires.

Je dois rédiger la conclusion. J'ai pensé à : Deux vecteurs directeurs RS et RT du plan RST et deux vecteurs directeurs EN et EA du plan ENA. D'où EN et RT sont colinéaires, donc (RST)//(ENA)