Déterminer équations de tangente et de cercle

Bonjour

Le plan est rapporté à un repère orthonormal (O,IJ). On considère les points A et B de coordonnées respectives (2.0) et (1/2,3/2)
On appelle C le cercle circonscrit au triangle OAB
4 Equation de la tangente en O à C

a) Déterminer une équation de la tangente en O à C
je pense avoire trouvé cette question :x+1/2y=0

b) De manière générale, montrer que la tangente en O à un cercle d’équation x²+y²+ax+by=0 a pour équation ax+by=0

On considère le point D(1,3) on se propose de déterminer les équations des tangentes à C issues de D

b) Soit T un point de C montré que la droite (DT) est tangente en T à C si et seulement si T appartient au cercle de diamètre [DI]
c) Ecrire une équation du cercle de diamètre [DI]
d) Montrer que les points de contact des tangentes à C issues de D sont les points dont les coordonnées (x,y) sont les solutions du système
(x²+y²-2x-y=0
(x²+y²-2x-7/2y +5/2=0

je n'arrive pas les questions 4b et 5b et 5c,merci d'avance (j'avou ne pas avoir trop compris ce chapitre ...)

Merci d'avance

Bonjour,

Question 4 b), Cherche les coordonnées du centre I du cercle, puis utilise le fait que la tangente est orthogonale au vecteur OI.

Quelle est la question 5 a) ?

okay merciii jvais essayer
la 5a c'était vérifier que D est extérieur a C et ça j'ai réussit à le prouver.

Pourrais-tu m'aider à répondre à la question 4b et, eventuellement, me donner des pistes pour les questions de la question 5 stp ?

As tu trouvé les coordonnées du centre du cercle ?

oui, j'ai trouvé I(1;1/2)

Comment as-tu trouvé ces valeurs, car l'équation du cercle est :
x²+y²+ax+by=0 ?

Pour trouver ce résultat, j'ai calculé le produit scalaire des vecteurs MI et OA , ce qui donne 2x-2=0 ( avec M milieu de [OA] ) puis le produit scalaire des vecteurs JI et AB, ce qui donne -3x+3y-9/2=0. ( avec J milieu de [AB] )
Puis, j'ai posé un système pour trouver la valeur de x ( 1 ) et de y ( 1/2 ).

A quoi corresponde ces points I et J ?

La question 4 b) est une démonstration de manière générale, sans prendre en compte le début de l'exercice.
A partir de l'équation du cercle, x²+y²+ax+by=0, tu dois trouver les coordonnées de son centre que l'on peut noter K ( Car I est donné pour le repère).

I est le centre du cercle C et j'ai appellé J le milieu du côté [AB] du triangle OAB.
J'ai déjà trouvé les coordonnées du centre du cercle, qui sont (1;1/2).

Tu ne peux pas utiliser les points I et J car ton repère c'est O; I, J.

C'est à la question 5 que tu réponds ?

Equation du cercle de diamètre [DI] ??

Dans l'énnoncé, on parle de vecteur i et non pas de I donc je peux utiliser les lettres I et J.
Non je ne réponds pas à la question 5. Je ne t'ai pas donné de réponse pour la question 5.

Donc pour la question 4b,
Indique en fonction de a et b les coordonnées du centre du cercle pour un cercle d'équation : x²+y²+ax+by=0
Ecrire cette équation sous la forme (x-x0)²+(y-y0)² = R²

Dans la question 5,

On indique diamètre [DI], Quelles sont les coordonnées du point I ?

Pourrais-tu être plus précise pour la question 4b stp ? Je ne comprends pas très bien..
Les coordonnées de I sont (1;1/2)

Dans le cas général x²+y²+ax+by=0

Il faut trouver les coordonnées de I centre de ce cercle en partant de

x²+y²+ax+by=0 essaye de trouver $x_I$ et $y_I$ tel que

$x-x_I$ )² + $y-y_I$ )² = R²

Pense à ce que tu as vu dans le chapitre sur la forme canonique .....

Merci Zorro mais cela me semble compliqué.

PAs tant que ça !

x² + ax = (x + ...)² - ??

y² + by = (y + ...)² - ??

Et tu mets tout cela ensemble

Merci pour ton aide précieuse Zorro. J'aurais peut-être encore besoin de toi ultérieurement.

Je t'en prie !

Je n'ai fait que de te redonner une indication que Noemi t'avait déjà donnée !

Peut-être mais je n'avais pas bien compris ce qu'elle m'avait dit. Merci

J'ai trouvé la réponse à la question 4b mais auparavant, il y a la question 3 qui me gène: Etude de l'intersection de C avec les horizontales. Déterminer, en fonction de m, le nombre de points d'intersection de C avec la droite d'équation y=m.
Pourrais-tu une nouvelle fois m'éclaircir ?

Avec un dessin et une règle qui représente les droites horizontales et qui se déplacerait de bas en haut ou de haut en bas , tu ne vois pas ce qu'on te demande ?

Si, j'ai très bien compris la question et j'ai même trouvé les réponses qui seraient environ -0.6 < ou égal à m < ou égal à 1.7 avec -0.6 et 1.7 les tangentes à C. Mais je ne sais pas du tout comment l'exprimer avec le calcul.

Est-ce qu'on parle de la même question ?

Tu réponds

"""environ -0.6 < ou égal à m < ou égal à 1.7 avec -0.6 et 1.7 "" à quelle question ?

Je réponds à la question que je t'ai envoyé, la question 3 qui, dans mon sujet, dit : Etude de l'intersection de C avec les horizontales. Déterminer, en fonction de m, le nombre de points d'intersection de C avec la droite d'équation y=m.
Je trouve ces réponses ( qui ne sont peut-être pas justes ) mais je ne vois pas comment le justifier.

Il faut trouver les coordonnées de C et D dans :

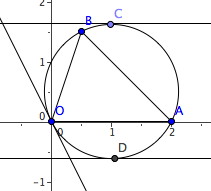
$fichier math$

Oui voila mais comment les trouver par le calcul ?

Je vais me déconnecter ! A plus !

D'accord. En tout cas, merci beaucoup Zorro. Tu portes bien ton pseudo: tu sauves les gens Bonne nuit

J'ai besoin une nouvelle fois d'aide pour la question 3 : Etude de l'intersection de C avec les horizontales. Déterminer, en fonction de m, le nombre de points d'intersection de C avec la droite d'équation y=m.
Ainsi que pour la question 4b svp ...

Pour la question 3;

Quelle est l'équation de la droite horizontale qui passe par :
le point C ?
le point D ?

Graphiquement,les points d'intersection entre le cercle C et la droite d'équation y=m sont les valeurs de m comprises entre -0.6 et 1.7 mais je ne sais pas comment le prouver par le calcul..

Quelles sont les données de l'énoncé ?

Peux-t-on avoir l'énoncé complet ?

Le plan est rapporté à un repère orthonormal (O,IJ). On considère les points A et B de coordonnées respectives (2.0) et (1/2,3/2)
On appelle C le cercle circonscrit au triangle OAB
1 On recherche l'équation de C
a) Déterminer le centre I de C
b) Vérifier que C a pour équation x²+y²-2x-y=0

Déterminer les coordonnées des points d'intersection de C avec les axes de coordonnées.
Etude de l'intersection de C avec les horizontales
Déterminer en fonction de m le nombre de points d'intersection de C avec la droite y=m
4 Equation de la tangente en O à C
a) Déterminer une équation de la tangente en O à C
b) De manière générale, montrer que la tangente en O à un cercle d'équation x²+y²+ax+by=0 a pour équation ax+by=0
On considère le point D(1,3) on se propose de déterminer les équations des tangentes à C issues de D
a) Vérifiez que D est extérieur à C
b) Soit T un point de C montré que la droite (DT) est tangente en T à C si et seulement si T appartient au cercle de diamètre [DI]
c) Ecrire une équation du cercle de diamètre [DI]
d) Montrer que les points de contact des tangentes à C issues de D sont les points dont les coordonnées (x,y) sont les solutions du système
(x²+y²-2x-y=0
(x²+y²-2x-7/2y +5/2=0
e) Résoudre le système ci-dessus
f) Déterminer les équations des tangentes à C issues de D

Voila Noémi.
Les questions 3 et 4b me posent problème, ainsi que la 5b.

Tu résous l'équation :
x²+y²-2x-y=0, avec y = m.

Oui donc cela me donne x²+m²-2x-y=0 mais comment résoudre cette équation ?

joséphine
Oui donc cela me donne x²+m²-2x-y=0 mais comment résoudre cette équation ?

L'équation est x² - 2x + m² - m = 0
C'est une équation du second degré de la forme x² -2x + a = 0

Comment tu résous une équation du second degré ?

Comment, de l'équation x² - 2x + m² - m = 0 arrives tu à placer ce a : x² -2x + a = 0 ?

J'ai juste remplacé m² - m par a pour te faire voir la forme de l'équation.
Résous l'équation :
x² - 2x + m² - m = 0

Donc résoudre l'équation x²-2x+m²-m=0 revient à résoudre x²-2x+a=0 ?