Etudier une suite définie par une intégrale

(re) bonjour, j'aurais besoin d'aide pour cet exo, merci.

u est la suite définie pour tout entier n ≥ 2 par:

Un= 1 +1/2 + ... + 1/n - $∫1n1/x,dx\int_{1}^{n} {1/x} ,\text{d}{x}$ .

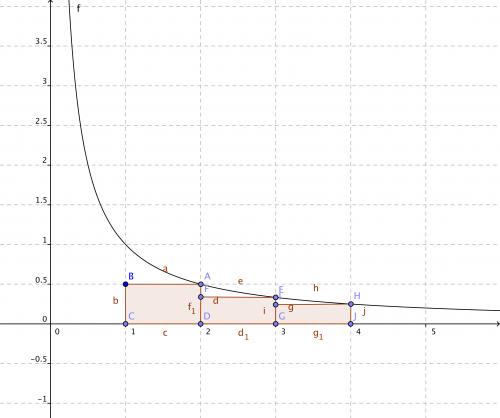
1)Construire dans un repère orthonormal la courbe représentative de la fonction x → 1/x sur ]0;+∞[.

2)a) Sur les intervalles [1;2] , [2;3] et [3;4], construire respectivement les rectangles R1, R2, R3 de hauteur 1/2; 1/3; 1/4 et les rectangles R'1, R'2 et R'3 de hauteur 1; 1/2; 1/3.

En déduire que 1/2 + 1/3 + 1/4 ≤ $∫141/x,dx\int_{1}^{4} {1/x} ,\text{d}{x}$ ≤ 1 + 1/2 + 1/3.

b) n est un entier tel que n ≥2. Montrer que 1/2 + 1/3 +...+ 1/n ≤ $∫1n1/x,dx\int_{1}^{n} {1/x} ,\text{d}{x}$ ≤ 1+ 1/2+ ... + 1/(n-1).

En déduire que pour tout entier n ≥2, 0≤Un≤1.

4)a) Démontrer que pour tout entier n ≥ 2, 1/(n+1) ≤ $∫nn+11/x,dx\int_{n}^{n+1} {1/x} ,\text{d}{x}$ ≤ 1/n.

b) En déduire que la suite u est décroissante.
c) Montrer que la suite u est convergente. On note C sa limite (le nombre C est appelé constante d’Euler).

5)v est la suite définie pour n ≥ 2 par Vn = Un - 1/n

a) Montrer à l’aide de la question 4)a) que les suites u et v sont adjacentes.
b) En déduire que pour tout entier n ≥ 2, 0≤Un-C≤1/n.

2)a) j'ai tracé la courbe, j'ai pris comme unité 1 cm = 0,2 cm. comment ça se passe pour construire les rectangles ?

Re Bonjour,
Pour les rectangles :
Sur l'intervalle [1;2], le rectangle à pour dimension largeur l'intervalle [1;2], hauteur 1/2 ;
Sur l'intervalle [2;3], le rectangle à pour dimension largeur l'intervalle [2;3], hauteur 1/3 ;
....

Tu compares ensuite les aires par rapport à la courbe.

il faut que je retrace la courbe, c'est mieux de prendre quoi comme unité ?

Prend 2 cm pour unité.

ok, j'ai tracé la courbe et les rectangles. bon après pour démontrer l'inéquation j'arrive pas trop

Que peux tu dire de la position de la courbe par rapport aux rectangles ?

Noemi
Que peux tu dire de la position de la courbe par rapport aux rectangles ?

d'après mon graphe, la courbe est en dessous des rectangles R1, R2, R3, R'1,R'2,R'3

Ce n'est pas possible,
dans un cas, tu dois être en dessous, 1/2 + 1/3 + 1/4; (R1, R2, R3)
et dans l'autre tu dois être au dessus 1 + 1/2 + 1/3 ; (R'1, R'2, R'3)

Vérifie ton tracé.

Le graphique avec les premiers rectangles.

ah, je me suis trompé quand j'ai tracé les rectangles. donc je comprend bien l'inéquation mais à chaque fois je ne sais pas démontrer

Pour le tracé que j'ai transmis, la somme des aires des rectangles est :
1/2 + 1/3 + 1/4
Tous les rectangles sont en dessous de la courbe, donc la somme est inférieure à l'intégrale.
Pour les autres rectangles, ils sont tous au dessus de la courbe, donc la somme est supérieure à l'intégrale.
D'ou l'écriture de l'inéquation.

Si on construit n rectangles, on en déduit l'inéquation à l'ordre n.

bonjour,

ok pour la question 2)a).

2)b) c'est la même inéquation sauf que c'est à l'ordre de n, donc l'inéquation est aussi vraie, comme tu as dit avant? mais comment justifier

Bonjour,

On considère juste que l'on étend à l'ordre n. La question est juste montrer .... et non démontrer.

ok.

donc je peut juste écrire, si on étend à l'ordre n l'inéquation 1/2 + 1/3 + 1/4 ≤ $∫141/x,dx\int_{1}^{4} {1/x} ,\text{d}{x}$ ≤ 1 + 1/2 + 1/3 on a 1/2 + 1/3 +...+1/n ≤ $∫1n1/x,dx\int_{1}^{n} {1/x} ,\text{d}{x}$ ≤ 1 + 1/2 +...+1/(n-1) ?

Oui,

C'est correct.

ok.

si la somme des aires des triangles R1;R2 et R3 est plus petites que l'intégrale, je ne comprend pas comment on peut avoir 0≤Un≤1

Tu sais que :
1/2 + 1/3 +...+ 1/n ≤ $∫1n1xdx\int_{1}^{n}{\frac{1}{x}dx}$
soit
1/2 + 1/3 +...+ 1/n - $∫1n1xdx\int_{1}^{n}{\frac{1}{x}dx}$ ≤ 0
Et
Un = 1 + 1/2 + 1/3 +...+ 1/n - $∫1n1xdx\int_{1}^{n}{\frac{1}{x}dx}$

Un = 1 + k ( avec k ≤ 0)
donc
Un ≤ 1

d'accord mais comment on sait que Un ≥ 0 ?

Pour Un ≥0, tu prends les deux termes de droite de l'inéquation.

Noemi
Pour Un ≥0, tu prends les deux termes de droite de l'inéquation.

quels termes ?

$∫1n1xdx≤1+12+13+.....1n−1\int_{1}^{n}{\frac{1}{x}dx}\leq 1+\frac{1}{2}+\frac{1}3{} + .....\frac{1}{n-1}$

Noemi
$∫1n1xdx≤1+12+13+.....1n−1\int_{1}^{n}{\frac{1}{x}dx}\leq 1+\frac{1}{2}+\frac{1}3{} + .....\frac{1}{n-1}$

je ne vois toujours pas pour montrer qu Un ≥0 :frowning2:

D'après l'inéquation précédente,
$1+12+13+....+1n−1−∫1nf(x)dx≥01+\frac{1}{2}+\frac{1}{3}+ .... + \frac{1}{n-1}-\int_{1}^{n}{f(x)dx}\geq 0$
donc
$1+12+13+....+1n−1+1n−∫1nf(x)dx≥01+\frac{1}{2}+\frac{1}{3}+ .... + \frac{1}{n-1}+\frac{1}{n}-\int_{1}^{n}{f(x)dx}\geq 0$

Noemi
D'après l'inéquation précédente,
$1+12+13+....+1n−1−∫1nf(x)dx≥01+\frac{1}{2}+\frac{1}{3}+ .... + \frac{1}{n-1}-\int_{1}^{n}{f(x)dx}\geq 0$
donc
$1+12+13+....+1n−1+1n−∫1nf(x)dx≥01+\frac{1}{2}+\frac{1}{3}+ .... + \frac{1}{n-1}+\frac{1}{n}-\int_{1}^{n}{f(x)dx}\geq 0$

je suis désolé mais je n'arrive pas à comprendre comme obtenir ça
d'après 1/2+1/3+...+1/n ≤ $∫1n1/x,dx\int_{1}^{n} {1/x} ,\text{d}{x}$ ≤ 1+1/2+...+1/(n-1).

Tu prends en compte que la dernière inéquation et tu fais passer l'intégrale à droite.

Noemi
Tu prends en compte que la dernière inéquation et tu fais passer l'intégrale à droite.

donc je me retrouve avec 1/2+1/3+...+1/n ≤ 1+1/2+...+ 1/(n-1) - $∫1n1/x,dx\int_{1}^{n} {1/x} ,\text{d}{x}$

Non

a ≤ b ≤ c équivalent ) a ≤ b et b≤ c
et si b≤ c alors c - b ≥ 0

Si tu soustrais b
a - b ≤ b - b ≤ c - b soit
a- c ≤ 0 ≤ c - b

Noemi
Non

a ≤ b ≤ c équivalent ) a ≤ b et b≤ c
et si b≤ c alors c - b ≥ 0

Si tu soustrais b
a - b ≤ b - b ≤ c - b soit
a- c ≤ 0 ≤ c - b

ah d'accord ! donc on a 1+1/2+...+ 1/(n-1) - $∫1n1/x,dx\int_{1}^{n} {1/x} ,\text{d}{x}$ ≥0. mais ce qui me gêne c'est 1/(n-1). pour Un on a 1/n ?

Tu ajoutes 1/n de part et d'autre de l'inégalité, cela fait ≥ 1/n donc ≥ 0 car n >0.

Noemi
Tu ajoutes 1/n de part et d'autre de l'inégalité, cela fait ≥ 1/n donc ≥ 0 car n >0.

d'accord.

4)a) on doit commencer par où

Ecris l'inégalité précédente à l'ordre n+1.

Noemi
Ecris l'inégalité précédente à l'ordre n+1.

et comment ça se fait que 1 1/2 1/3 ... disparaissent ?

Ecris l'inégalité précédente à l'ordre n+1.
Puis tu soustrais les deux inéquations.

à gauche : 1/2 + 1/3 +...+ 1/(n+1) - 1/2 - 1/3 -1/n
à droite : 1 + 1/2 + 1/n - 1 -1/2 - 1/(n-1) ?

Donc il reste à gauche 1/(n+1) et à droite 1/n
au centre l'intégrale de 1/x pour x variant de n à n+1.

Pour la décroissance de la suite tu calcule
$U$ _{n+1} $U_n$ en utilisant l'inéquation.

Noemi
Donc il reste à gauche 1/(n+1) et à droite 1/n
au centre l'intégrale de 1/x pour x variant de n à n+1.

Pour la décroissance de la suite tu calcule
$U$ _{n+1} $U_n$ en utilisant l'inéquation.

ok, mais un moment on a , 1/(n+1) - 1/n ≤ $∫1n+11/x,dx\int_{1}^{n+1} {1/x} ,\text{d}{x}$ ≤ 1/n - 1/(n+1)

comment on arrive à 1/(n+1)≤ $∫1n+11/x,dx\int_{1}^{n+1} {1/x} ,\text{d}{x}$ ≤ 1/n ?

Tu as :
$\leq \int_{1}^{n+1}{1/xdx}\leq 1+1/2+1/3+ ....+ 1/(n-1)+1/n$
et
$\leq \int_{1}^{n}{1/xdx}\leq 1+1/2+1/3+ ....+ 1/(n-2)+1/(n-1)$
Si tu soustrais
$\leq \int_{n}^{n+1}{1/xdx}\leq 1/n$

il y a des termes que je ne vois pas d'où ils sortent. donc je vais essayer de reprendre.

1/2+1/3+...+1/n ≤ $∫1n1/x,dx\int_{1}^{n} {1/x} ,\text{d}{x}$ ≤ 1+1/2+...+1/(n-1)

ça c'est l'inéquation de départ pour la question 4)a). donc tu m'a dit de mettre cette inéquation à l'ordre de n+1 donc ça donne :

1/2+1/3+...+1/(n+1) ≤ $∫1n+11/x,dx\int_{1}^{n+1} {1/x} ,\text{d}{x}$ ≤ 1+1/2+...+1/n

après tu m'a dit de soustraire ces 2 inéquations :

1/(n+1)-1/n ≤ $∫1n+11/x,dx\int_{1}^{n+1} {1/x} ,\text{d}{x}$ ≤ 1/n-1/(n-1)

après je sais pas. c'est bien ça jusqu'ici ? pace que la je suis vraiment paumé

Non,

Tu fais la même erreur

1/2 + 1/3 + 1/4 + ......+ 1/n
les .... veulent indiquer que l'on effectue la somme jusqu'à la valeur n
Par exemple si n = 10
1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 + 1/10
Donc le terme avant 1/n c'est 1/(n-1)
et celui avant 1/(n-1) c'est 1/(n-2)

J'ai indiqué le résultat dans mon précédent post.

Noemi
Tu as :
$\leq \int_{1}^{n+1}{1/xdx}\leq 1+1/2+1/3+ ....+ 1/(n-1)+1/n$
et
$\leq \int_{1}^{n}{1/xdx}\leq 1+1/2+1/3+ ....+ 1/(n-2)+1/(n-1)$
Si tu soustrais
$\leq \int_{n}^{n+1}{1/xdx}\leq 1/n$

donc ok. mais tu soustrais quels membres avec quals membres parceque je n'obtiens pas le même résultat