Devoir maison - Angles et Trigonométrie
-
Mmimidu11 dernière édition par
Bonjour, j'ai un devoir maison à rendre mercredi prochain, je l'ai commencé et je bloque sur la suite de cet exercice. Pourriez-vous m'aider, m'expliquer ce qu'il y a à faire ?
Merci beaucoup d'avance.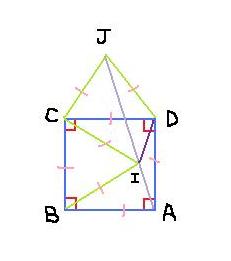
Enoncé :
ABCD est un carré tel que (ad⃗;ab⃗)=π/2(\vec{ad};\vec{ab})= \pi /2(ad;ab)=π/2
BIC et CDJ sont des triangles équilatéraux directs.
1°) Dans les triangles isocèles, ADJ, ABI et DCI, donner la mesure principale des angles orientés : (dj⃗;da⃗)(\vec{dj};\vec{da})(dj;da) , (ba⃗;bi⃗)(\vec{ba};\vec{bi})(ba;bi) , (ci⃗;cd⃗)(\vec{ci};\vec{cd})(ci;cd)
En déduire la mesure principale des angles à la base de ces triangles, pris dans le sens direct.
2°)a) Déterminer la mesure principale de (ia⃗;id⃗)(\vec{ia};\vec{id})(ia;id).
b) En déduire la mesure principale de (ad⃗;(ai⃗)(\vec{ad};(\vec{ai})(ad;(ai).
3°) Comparer avec la mesure de (ad⃗;aj⃗)(\vec{ad};\vec{aj})(ad;aj) trouvée dans la question 1°
Qu'en déduit-on pour les points A, I et J ?Exercice :
1°)
Pour (dj⃗;da⃗)(\vec{dj}; \vec{da})(dj;da) :
On sait que adc^=π/2\hat{adc}= \pi /2adc^=π/2 et cdj^=π/3\hat{cdj}= \pi /3cdj^=π/3
π/2+π/3=(3π+2π)/6=5π/6\pi /2+\pi /3=(3\pi +2\pi )/6=5\pi /6π/2+π/3=(3π+2π)/6=5π/6
La mesure principale de (dj⃗;da⃗)(\vec{dj}; \vec{da})(dj;da) est de 5π/65\pi /65π/6Pour (ba⃗;bi⃗)(\vec{ba}; \vec{bi})(ba;bi) :
On sait qu'un angle droit vaut π/2\pi /2π/2 et qu'un angle d'un triangle équilatéral vaut π/3\pi /3π/3.
π/2−π/3=(3π−2π)/6=π/6\pi /2 -\pi /3=(3\pi -2\pi )/6= \pi /6π/2−π/3=(3π−2π)/6=π/6
La mesure principale de (ba⃗;bi⃗)(\vec{ba}; \vec{bi})(ba;bi) est de π/6\pi /6π/6.Pour (ba⃗;bi⃗)(\vec{ba}; \vec{bi})(ba;bi) :
On sait qu'un angle droit vaut π/2\pi /2π/2 et qu'un angle d'un triangle équilatéral vaut π/3\pi /3π/3.
π/2−π/3=(3π−2π)/6=π/6\pi /2 -\pi /3=(3\pi -2\pi )/6= \pi /6π/2−π/3=(3π−2π)/6=π/6
La mesure principale de (ba⃗;bi⃗)(\vec{ba}; \vec{bi})(ba;bi) est de π/6\pi /6π/6.Et là je bloque pour la suite de l'exercice, je n'arrive pas à trouver comment faire pour avoir la mesure des angles à la base des triangles, et ce n'est pas faute d'avoir essayer.
Merci pour votre aide
-
Bonjour,
Pour la question 2) Quelle est la nature du triangle ADJ ?
-
Mmimidu11 dernière édition par
C'est un triangle isocèle en I
-
Ma question porte sur le triangle ADJ et non ADI.
Mais ADJ est aussi isocèle donc l'angle (AD,AI)
-
Mmimidu11 dernière édition par
Je ne suis plus là ...
-
Mmimidu11 dernière édition par
Le début que j'ai fait est correct ou pas ?
-
Mmimidu11 dernière édition par
Pouvez-vous m'expliquer tout svp, j'ai beacoup de mal à comprendre
-
Le triangle ADJ est isocèle et tu connais la mesure de l'angle (DJ, DA) donc tu peux calculer la mesure des deux autres angles.
Tu appliques le même raisonnement pour le triangle ADI.
-
Mmimidu11 dernière édition par
Donc
On sait que dans le triangle ABI, b^\hat{b}b^ vaut π/6\pi /6π/6 car cba^=π/2\hat{cba}= \pi /2cba^=π/2 et cbi^=π/3\hat{cbi}= \pi /3cbi^=π/3 (π/2−π/3=π/6)(\pi /2-\pi /3=\pi /6)(π/2−π/3=π/6). Or dans un triangle, la somme des trois angles vaut π\piπ. Les deux angles à la base sont égaux puisque ABI est un triangle isocèle en B. Donc (ai⃗;ab⃗)=(ib⃗;ia⃗)(\vec{ai};\vec{ab}) = (\vec{ib};\vec{ia})(ai;ab)=(ib;ia).
Donc 2∗(ai⃗;ab⃗)=π−π/6=6π/6−π/6=5π/62*(\vec{ai};\vec{ab})= \pi-\pi /6=6\pi /6-\pi /6=5\pi /62∗(ai;ab)=π−π/6=6π/6−π/6=5π/6. Et (ai⃗;ab⃗)=(ib⃗;ia⃗)=(5π/6)/2=(5π/6)/(2/1)=5π/6∗1/2=5π/12(\vec{ai};\vec{ab})=(\vec{ib};\vec{ia})=(5\pi /6)/2=(5\pi /6)/(2/1)=5\pi /6*1/2=5\pi /12(ai;ab)=(ib;ia)=(5π/6)/2=(5π/6)/(2/1)=5π/6∗1/2=5π/12
La mesure principale des angles à la base du triangle ABI est 5π/125\pi /125π/12On sait que dans le triangle DCI, c^\hat{c}c^ vaut π/6\pi /6π/6 car dcb^=π/2\hat{dcb} = \pi /2dcb^=π/2 et icb^=π/3\hat{icb} = \pi /3icb^=π/3 (π/2−π/3=π/6)(\pi /2-\pi /3=\pi /6)(π/2−π/3=π/6). Or dans un triangle, la somme des trois angles vaut π\piπ. les deux angles à la base sont égaux puisque DCI est un triangle isocèle en C.
Donc (dc⃗;di⃗)=(id⃗;ic⃗)(\vec{dc};\vec{di}) = (\vec{id};\vec{ic} )(dc;di)=(id;ic). Donc 2∗(dc⃗;di⃗)=π−π/6=6π/6−π/6=5π/62*(\vec{dc};\vec{di})= \pi-\pi /6=6\pi /6-\pi /6=5\pi /62∗(dc;di)=π−π/6=6π/6−π/6=5π/6. Et (dc⃗;di⃗)=(id⃗;ic⃗)=(5π/6)/2=(5π/6)/(2/1)=5π/6∗1/2=5π/12(\vec{dc};\vec{di})=(\vec{id};\vec{ic})=(5\pi /6)/2=(5\pi /6)/(2/1)=5\pi /6*1/2=5\pi /12(dc;di)=(id;ic)=(5π/6)/2=(5π/6)/(2/1)=5π/6∗1/2=5π/12.
La mesure principale des angles à la base du triangle DCI est 5π/125\pi /125π/12.On sait que dans le triangle ADJ, d^=5π/6\hat{d}= 5\pi /6d^=5π/6 car adc^=π/2\hat{adc}= \pi /2adc^=π/2 et jdc^=π/3\hat{jdc}= \pi /3jdc^=π/3 (π/2+π/3=5π/6)(\pi /2+\pi /3=5\pi /6)(π/2+π/3=5π/6). Or dans un triangle, la somme des trois angles vaut π\piπ. Les deux angles à la base sont égaux puisque ADJ est un triangle isocèle en D.
Donc (ad⃗;aj⃗)=(ja⃗;jd⃗)(\vec{ad};\vec{aj})=(\vec{ja};\vec{jd})(ad;aj)=(ja;jd). Donc 2∗(ad⃗;aj⃗)=π−5π/6=6π/6−5π/6=π/62*(\vec{ad};\vec{aj})=\pi -5\pi /6=6\pi /6-5\pi /6=\pi /62∗(ad;aj)=π−5π/6=6π/6−5π/6=π/6. Et (ad⃗;aj⃗)=(ja⃗;jd⃗)=(π/6)/2=(π/6)/(2/1)=π/6∗1/2=π/12(\vec{ad};\vec{aj})=(\vec{ja};\vec{jd})=(\pi /6)/2=(\pi /6)/(2/1)=\pi /6*1/2=\pi /12(ad;aj)=(ja;jd)=(π/6)/2=(π/6)/(2/1)=π/6∗1/2=π/12.
La mesure principale des angles à la base du triangle ADJ est π/12\pi /12π/12.Est-ce juste ?
Merci
-
Mmimidu11 dernière édition par
2°)a)
On sait que dans le triangle IAD, a^=π/12\hat{a} = \pi /12a^=π/12. or dans un triangle, la somme des trois angles vaut π\piπ. Les deux angles à la base (a^\hat{a}a^ et d^\hat{d}d^) saont égaux puisque IAD est un triangle ispcèle en I.
Donc a^=d^=π/12\hat{a}=\hat{d}=\pi /12a^=d^=π/12. Donc π/12∗2=π/6\pi /12*2=\pi /6π/12∗2=π/6. Donc π−π/6=6/π6−/π6=5π/6\pi-\pi /6=6/\pi 6-/\pi 6=5\pi /6π−π/6=6/π6−/π6=5π/6
La mesure principale de (ia⃗;id⃗)(\vec{ia}; \vec{id})(ia;id) est 5π/65\pi /65π/6.b)
On a démontrer dans la question 1° que dans le triangle ADJ a^=π/12\hat{a} = \pi /12a^=π/12. donc dans le triangle DAI a^=π/12\hat{a} = \pi /12a^=π/12. Donc la mesure principale de (ad⃗;ai⃗)(\vec{ad};\vec{ai})(ad;ai) est π/12\pi /12π/12.
3°)
(ad⃗;ai⃗)=π/12(\vec{ad};\vec{ai})=\pi /12(ad;ai)=π/12
(ad⃗;aj⃗)=π/12(\vec{ad};\vec{aj})=\pi /12(ad;aj)=π/12
Les deux couples de vecteurs sont égaux (ils ont la même mesure principale). On en déduit donc que les points A, I et J sont alignés.Mon exercice est-il juste depuis le début ?
Merci beaucoup d'avance
-
As-tu démontré que le triangle IAD est isocèle en I ?