Etudier les variations et les extremums d'une fonction de second degré

Bonjour,
j'ai un DM de maths à faire et j'ai fait les premières questions mais je ne sais pas si mes résultats sont justes. Je bloque pour les deux dernières questions. Pouvez vous m'aider s'il vous plaît ?

Dans un plan muni d'un repère orthonormé (O;;), on considère la courbe C d'équation y = x et le point A(2;0).
L'objet de ce problème est de déterminer le point de C qui est le plus proche de A.

1)Soit x un réel positif et M le point de la courbe C d'abscisse x. Exprimer AM en fonction de x.
--> AM² = Ax² + xM²
= (x-2)² + y²
= (x-2)² + x

Soit f la fonction définie sur l'intervalle [0;+∞[ par: f(x) = (x- 3/2)² + 7/4

Quelle relation existe-t-il entre AM et f(x) ?
--> AM² = f(x)

Je ne sais pas si je dois justifier par quelque chose pour le 1) et le 2).

Déterminer les variations de la fonction f sur l'intervalle [0;+∞[.
--> x ≤ y sur [0;+∞[
x + 3/2 ≤ y + 3/2
(x + 3/2)² ≤ (y + 3/2)²
(x + 3/2)² + 7/4 ≤ (y + 3/2)² + 7/4
f(x) ≤ f(y)
Donc f est croissante sur [0;+∞[.

4)a.En déduire les variations de la distance AM en fonction de x.
b.Quelles sont les coordonnées du point M pour lequel la distance AM est minimal ? préciser la valeur de ce minimun.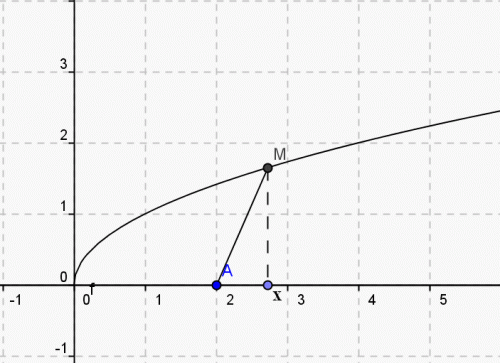

$fichier math$

Merci d'avance !

Bonjour,

Pour la question 2), tu dois montrer que f(x) = AM² en développant les expressions par exemple.

Question 3) les variations sont fausses.
Rectifie.

Je ne vois pas ce qu'il y a de faux pour les variations de f

Ce n'est pas :
x + 3/2 ≤ y + 3/2
mais
x - 3/2 ≤ y - 3/2

Tu peux élever au carré et ne pas changer le signe que si les deux termes sont positifs !

Ah okay.
donc:
x ≤ y sur [0;+∞[
x - 3/2 ≤ y - 3/2
(x - 3/2)² ≤ (y - 3/2)² le signe ne change pas puisqu'on est dans [0;+∞[
(x - 3/2)² + 7/4 ≤ (y - 3/2)² + 7/4
f(x) ≤ f(y)

J'ai développé AM² = x² - 3x + 4, est ce que cette forme je dois la mettre dans le 1) où le fait de m’arrêter à (x-2)² + x suffit pour répondre à la question ?

Tu peux écrire :
x - 3/2 ≤ y - 3/2
(x - 3/2)² ≤ (y - 3/2)² que si x et y ≥ 3/2.

A partir de f(x) = (x- 3/2)² + 7/4, cherche le minimum.

Pour la question 2), développe aussi f(x).

pour la 2) j'ai trouvé f(x) = x² -3x + 4

euh je fais comment pour la 4)a. ?

Le minimum est 3/2.

Quelles sont les variations de la fonction x² ?

décroissant sur ]-∞;0] et croissant sur [0;+∞[.
Mais pourquoi la fonction x²
je ne comprends pas

Car la fonction : f(x) = (x- 3/2)² + 7/4
est de la forme X² + 7/4,
donc variation similaire à x²
décroissante de 0 à 3/2, puis croissante de 3/2 à +∞.

ah okay
donc, les variations de AM en fonction de x sont décroissante de [0;3/2], puis croissante de [3/2;+∞].

Oui.