DM première S sur les barycentres et trigonométrie
-
FFilou900 dernière édition par
Bonjour à tous,
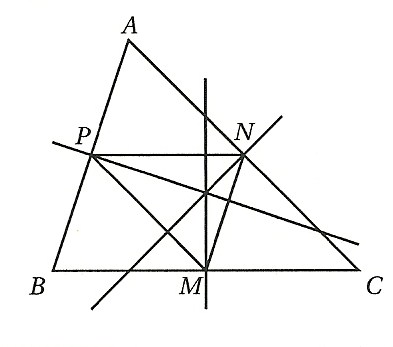
J'ai un DM à faire et je bloque à la deuxième question de la dernière partie. Pourriez-vous me donner quelques pistes s'il vous plait pour me débloquer et finir ce DM (je ne demande pas la réponse, bien entendu il n'est pas question de ça, juste d'un petit coup de pouce). Voici l'énoncé ainsi qu'une photo illustrant la figure.
Soit ABC un triangle (A, B et C sont supposés distincts). On note a=BC, b=AC et c=AB
On sait d'après le cours que le centre de gravité G de ABC est l'isobarycentre de ABC. L'objectif de ce devoir est de trouvé des réels affectés aux points A,B et C tels que le centre I du cercle inscrit, l'orthocentre H ou le centre O du cercle circonscrit soit le barycentre des sommets.Partie C :
- Démontrer que les médiatrices du triangle ABC sont les hauteurs du triangle MNP.
- Démontrer que les angles du triangle MNP sont tous aigus.
- Exprimer O, centre du cercle circonscrit à ABC, comme barycentre de M,N,P.
- En déduire que O est le barycentre de A,B et C, affectés de coefficients à préciser.
Merci beaucoup d'avance pour votre aide.

-
Bonsoir,
Compare les angles des différents triangles composant le triangle ABC.
-
FFilou900 dernière édition par
Re bonsoir,
J'ai fait d'apres les angles correspondants et je trouve :
BMP+MPO=90°
APN+APO=90°CNO+MNO=90°
ANP+ANO=90°BMP+PMO=90°
CMN+NMO=90°A partir de ceci peut-on en conclure que PMN est inférieur ou égale à 90° tout comme PNM et NPM? Si la somme de deux angles est égales à 90°, l'un des angles est forcément inférieur ou égal à 90°.

-
Compare les angles des triangles ABC et MNP.
-
FFilou900 dernière édition par
Les angles des triangles ABC et MNP sont égaux et comme ABC a 3 angles aigus MNP a aussi 3 angles aigus.
-
Oui, c'est correct.
-
FFilou900 dernière édition par
Merci beaucoup. Quant au barycentre O= Bar {(M; tan A); (N; tan B); (P; tan C)} car O est le cercle circonscrit à ABC et O est aussi l'orthocentre du triangle MNP. Cela est-il exacte et cette justification suffit-elle?
-
FFilou900 dernière édition par
Pourriez vous m'aider pour la dernière question s'il vous plait, c'est assez urgent. Merci