Exercice trigonométrie dans un pentagone

Bonjour tout le monde !!!!!
Voilà, j'ai un exercice de maths, et je n'arrive pas à le résoudre :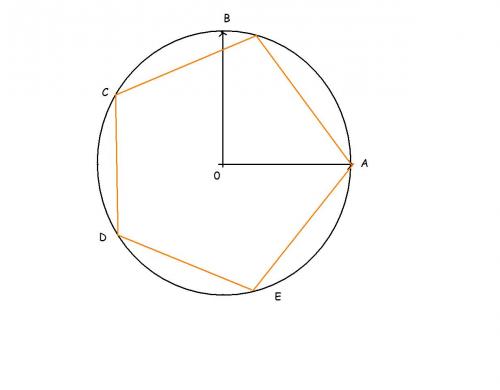

$fichier math$

Justifier que (OA,OB) = 2pi/5, (OA,OC) = 4pi/5, (OA,OD) = 6pi/5 et (OA,OE) = 8pi/5
En déduire les coordonnées de A,B,C,D et E puis celle V=OA+OB+OC+OD+OE (ce sont des vecteurs)
MOntrer que ( OB + OE ) et ( OC + OD ) sont colinéaires à OA puis que V est colinéaire à OA
Montrer de meme que V est colinéaire à OB à OC ,OD et à OE
a) En déduire que :
OA+OB+OC+OD+OE=0
b)1+2cos 2PI/5 + 2cos 4PI/5 = 0
En déduire que cos 2PI/5 est solution de l'équation 4x²+2x-1=0
Déterminer la valeur exacte de cos2pi/5

Pourriez-vous mes donner des indications pour pouvoir le résoudre
Merci d'avance pour vos réponses !!!!

Bonsoir,

A quoi correspond un angle de mesure 2π ?

Combien peut-on construire dans le pentagone de triangle identique au triangle OAB ?

Bonsoir,

2pi, c'est égal à 360°, un tour en gros
Pour le nombre de triangles, je ne sais pas, mais sa ne dois pas servir je pense

A ton avis, si je pose la question ?

Pardon, Normalement, tu dois pouvoir en faire 4

Non 5
et 2π diviser par 5 donne ....

oui 5, mais si tu regardes bien sur la figure, B est n'est pas situé sur un sommet du pentagone, je ne sais pas si c'est fait exprés ou pas
2pi/5 = 72°

A mon avis, c'est une erreur, puisqu'on demande de justifier que (OA,OB) = 2π/5

Oui, certainement, c'est ce qu'il me semblait, mais le dessin sert juste à illustrer la situation, pour mieux comprendre